Diferencia entre revisiones de «Poliedros arquimedeanos»
La enciclopedia de ciencias y tecnologías en Argentina
m |
m |
||
| Línea 1: | Línea 1: | ||
| − | Los '''poliedros arquimedianos''' son poliedros convexos cuyas caras son polígonos regulares (no todas idénticas, ya que se excluyen los 5 sólidos platónicos), cuyas aristas son todas de igual longitud y las configuraciones de cuyos vértices (forma de encuentro de las caras) son | + | Los '''poliedros arquimedianos''' son poliedros convexos cuyas caras son polígonos regulares (no todas idénticas, ya que se excluyen los 5 sólidos platónicos), cuyas aristas son todas de igual longitud y las configuraciones de cuyos vértices (forma de encuentro de las caras) son congruentes (pueden superponerse mediante adecuadas traslaciones, rotaciones y reflexiones). Esto permite construirlos de manera sencilla con el método que se describe al final del artículo. Los ''poliedros arquimedianos'' son 15, donde 2 de ellos son enantiomorfos con otros 2. El número que satisface la definición inicial es en realidad infinito porque incluye todos los prismas y antiprismas rectos cuyas bases son cualquiera de los infinitos polígonos regulares. Por esta razón es usual, aunque no hay consenso generalizado al respecto, excluir estos prismas y antiprismas de la lista de ''poliedros arquimedianos''. Salvo el icosaedro truncado —que tiene aplicaciones prácticas como cúpulas geodésicas y pelotas de fútbol— estos cuerpos son de interés más por su bella e intrigante forma y sus ricas propiedades geométricas que por su utilidad. |
| Línea 17: | Línea 17: | ||
|Rombicuboctaedro<br/>o rombicuboctaedro menor ||[[Archivo:Rhombicuboctahedron.jpg|60px]]<br/>:[[Archivo:Rhombicuboctahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|26 ||18 cuadrados + 8 triángulos equiláteros ||align=right|48 ||3·4·4·4 ||align=right|24 ||align=center|O<sub>h</sub> | |Rombicuboctaedro<br/>o rombicuboctaedro menor ||[[Archivo:Rhombicuboctahedron.jpg|60px]]<br/>:[[Archivo:Rhombicuboctahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|26 ||18 cuadrados + 8 triángulos equiláteros ||align=right|48 ||3·4·4·4 ||align=right|24 ||align=center|O<sub>h</sub> | ||
|- | |- | ||
| − | |Cuboctaedro truncado<br/>o rombicuboctaedro mayor ||[[Archivo:Truncatedcuboctahedron.jpg|60px]]<br/>:[[Archivo:Truncatedcuboctahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|26 ||6 octógonos regulares + 8 exágonos regulares + 12 cuadrados ||align=right|72 ||4·6·8 ||align=right|48 ||align=center|O<sub>h</sub> | + | |Cuboctaedro truncado<br/>o rombicuboctaedro mayor ||[[Archivo:Truncatedcuboctahedron.jpg|60px]]<br/>:[[Archivo:Truncatedcuboctahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|26 ||6 octógonos regulares + 8 exágonos regulares + 12 cuadrados ||align=right|72 ||4·6·8 + 4·8·6 ||align=right|48 ||align=center|O<sub>h</sub> |
|- | |- | ||
|Cubo romo <br/>o cuboctaedro romo<br/>(2 enantiomorfos) ||[[Archivo:Snubhexahedronccw.jpg|60px]]<br/>:[[Archivo:Snubhexahedronccw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]]<br/>[[Archivo:Snubhexahedroncw.jpg|60px]]<br/>:[[Archivo:Snubhexahedroncw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|38 ||6 cuadrados + 32 triángulos equiláteros ||align=right|60 ||3·3·3·3·4 ||align=right|24 ||align=center|O | |Cubo romo <br/>o cuboctaedro romo<br/>(2 enantiomorfos) ||[[Archivo:Snubhexahedronccw.jpg|60px]]<br/>:[[Archivo:Snubhexahedronccw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]]<br/>[[Archivo:Snubhexahedroncw.jpg|60px]]<br/>:[[Archivo:Snubhexahedroncw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|38 ||6 cuadrados + 32 triángulos equiláteros ||align=right|60 ||3·3·3·3·4 ||align=right|24 ||align=center|O | ||
| Línea 29: | Línea 29: | ||
|Rombicosidodecaedro<br/>o rombicosidodecaedro menor ||[[Archivo:Rhombicosidodecahedron.jpg|60px]]<br/>:[[Archivo:Rhombicosidodecahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|62 ||12 pentágonos regulares + 30 cuadrados + 20 triángulos equiláteros ||align=right|120 ||3·4·5·4 ||align=right|60 ||align=center|I<sub>h</sub> | |Rombicosidodecaedro<br/>o rombicosidodecaedro menor ||[[Archivo:Rhombicosidodecahedron.jpg|60px]]<br/>:[[Archivo:Rhombicosidodecahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|62 ||12 pentágonos regulares + 30 cuadrados + 20 triángulos equiláteros ||align=right|120 ||3·4·5·4 ||align=right|60 ||align=center|I<sub>h</sub> | ||
|- | |- | ||
| − | |Icosidodecaedro truncado<br/>o rombicosidodecaedro mayor ||[[Archivo:Truncatedicosidodecahedron.jpg|60px]]<br/>:[[Archivo:Truncatedicosidodecahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|62 ||12 decágonos regulares + 20 exágonos regulares + 30 cuadrados ||align=right|180 ||4·6·10 ||align=right|120 ||align=center|I<sub>h</sub> | + | |Icosidodecaedro truncado<br/>o rombicosidodecaedro mayor ||[[Archivo:Truncatedicosidodecahedron.jpg|60px]]<br/>:[[Archivo:Truncatedicosidodecahedron.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|62 ||12 decágonos regulares + 20 exágonos regulares + 30 cuadrados ||align=right|180 ||4·6·10 + 4·10·6 ||align=right|120 ||align=center|I<sub>h</sub> |
|- | |- | ||
|Dodecaedro romo<br/>o icosidodecaedro romo<br/>(2 enantiomorfos) ||[[Archivo:Snubdodecahedronccw.jpg|60px]]<br/>:[[Archivo:Snubdodecahedronccw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]]<br/>[[Archivo:Snubdodecahedroncw.jpg|60px]]<br/>:[[Archivo:Snubdodecahedroncw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|92 ||12 pentágonos regulares + 80 triángulos equiláteros ||align=right|150 ||3·3·3·3·5 ||align=right|60 ||align=center|I | |Dodecaedro romo<br/>o icosidodecaedro romo<br/>(2 enantiomorfos) ||[[Archivo:Snubdodecahedronccw.jpg|60px]]<br/>:[[Archivo:Snubdodecahedronccw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]]<br/>[[Archivo:Snubdodecahedroncw.jpg|60px]]<br/>:[[Archivo:Snubdodecahedroncw.gif|thumb|<small><center>'''Vea animación.'''</center></small>]] ||align=right|92 ||12 pentágonos regulares + 80 triángulos equiláteros ||align=right|150 ||3·3·3·3·5 ||align=right|60 ||align=center|I | ||
Revisión del 23:17 10 feb 2012
Los poliedros arquimedianos son poliedros convexos cuyas caras son polígonos regulares (no todas idénticas, ya que se excluyen los 5 sólidos platónicos), cuyas aristas son todas de igual longitud y las configuraciones de cuyos vértices (forma de encuentro de las caras) son congruentes (pueden superponerse mediante adecuadas traslaciones, rotaciones y reflexiones). Esto permite construirlos de manera sencilla con el método que se describe al final del artículo. Los poliedros arquimedianos son 15, donde 2 de ellos son enantiomorfos con otros 2. El número que satisface la definición inicial es en realidad infinito porque incluye todos los prismas y antiprismas rectos cuyas bases son cualquiera de los infinitos polígonos regulares. Por esta razón es usual, aunque no hay consenso generalizado al respecto, excluir estos prismas y antiprismas de la lista de poliedros arquimedianos. Salvo el icosaedro truncado —que tiene aplicaciones prácticas como cúpulas geodésicas y pelotas de fútbol— estos cuerpos son de interés más por su bella e intrigante forma y sus ricas propiedades geométricas que por su utilidad.
Rasgos
| Nombre | Imagen | Caras | Tipos de caras | Vértices | Ángulos en vértices | Aristas | Grupo puntual |
|---|---|---|---|---|---|---|---|
| Tetraedro truncado | 60px : Archivo:Truncatedtetrahedron.gif |
8 | 4 exágonos regulares 4 triángulos equiláteros |
18 | 3·6·6 | 12 | Td |
| Cuboctaedro | 60px + : Archivo:Cuboctahedron.gif |
14 | 6 cuadrados + 8 triángulos equiláteros | 24 | 3·4·3·4 | 12 | Oh |
| Cubo truncado | 60px : Archivo:Truncatedhexahedron.gif |
14 | 6 octógonos regulares + 8 triángulos equiláteros | 36 | 3·8·8 | 24 | Oh |
| Octaedro truncado | 60px : Archivo:Truncatedoctahedron.gif |
14 | 8 exágonos regulares + 6 cuadrados | 36 | 4·6·6 | 24 | Oh |
| Rombicuboctaedro o rombicuboctaedro menor |
60px : Archivo:Rhombicuboctahedron.gif |
26 | 18 cuadrados + 8 triángulos equiláteros | 48 | 3·4·4·4 | 24 | Oh |
| Cuboctaedro truncado o rombicuboctaedro mayor |
60px : Archivo:Truncatedcuboctahedron.gif |
26 | 6 octógonos regulares + 8 exágonos regulares + 12 cuadrados | 72 | 4·6·8 + 4·8·6 | 48 | Oh |
| Cubo romo o cuboctaedro romo (2 enantiomorfos) |
60px : Archivo:Snubhexahedronccw.gif 60px : Archivo:Snubhexahedroncw.gif |
38 | 6 cuadrados + 32 triángulos equiláteros | 60 | 3·3·3·3·4 | 24 | O |
| Icosidodecaedro | 60px : Archivo:Icosidodecahedron.gif |
32 | 12 pentágonos regulares + 20 triángulos equiláteros | 60 | 3·5·3·5 | 30 | Ih |
| Dodecaedro truncado | 60px : Archivo:Truncateddodecahedron.gif |
32 | 12 decágonos regulares + 20 triángulos equiláteros | 90 | 3·10·10 | 60 | Ih |
| Icosaedro truncado | 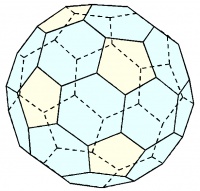 |
32 | 20 exágonos regulares + 12 pentágonos regulares | 90 | 5·6·6 | 60 | Ih |
| Rombicosidodecaedro o rombicosidodecaedro menor |
60px : Archivo:Rhombicosidodecahedron.gif |
62 | 12 pentágonos regulares + 30 cuadrados + 20 triángulos equiláteros | 120 | 3·4·5·4 | 60 | Ih |
| Icosidodecaedro truncado o rombicosidodecaedro mayor |
60px : Archivo:Truncatedicosidodecahedron.gif |
62 | 12 decágonos regulares + 20 exágonos regulares + 30 cuadrados | 180 | 4·6·10 + 4·10·6 | 120 | Ih |
| Dodecaedro romo o icosidodecaedro romo (2 enantiomorfos) |
60px : Archivo:Snubdodecahedronccw.gif 60px : Archivo:Snubdodecahedroncw.gif |
92 | 12 pentágonos regulares + 80 triángulos equiláteros | 150 | 3·3·3·3·5 | 60 | I |
Fuentes
- Ghyka, Matila; Estética de las pentágonos regularesoporciones en la naturaleza y en las artes; Editorial Poseidón; ciudad de Buenos Aires; 1953; Ghyka EPNA; pp. 87‑95.
- Archimedean solid en Wikipedia en inglés.