Enseñanza del concepto de área
La enciclopedia de ciencias y tecnologías en Argentina
El concepto de área está tan vinculado a nuestras actividades cotidianas que tomar conciencia de él es tan difícil como percibir el aire que respiramos. Su origen es tan viejo como la humanidad, pero su formulación matemática precisa, lograda recién cuatro siglos atrás, es hoy sólo patrimonio de unos pocos profesionales de las ciencias exactas. Para terminar con esta indeseable situación hay que modificar la enseñanza del concepto de área desde la escuela primaria. El presente artículo, cuyo autor es Carlos E. Solivérez, propone una manera de hacerlo.
Contenido
Introducción
- ¿Cuántos pliegos de cartulina debemos tener para poder hacer 25 sombreritos para la fiesta de cumpleaños?
- ¿Cuántos mosaicos hay que comprar para reemplazar el piso de la cocina?
- ¿Qué cantidad de tela se requiere para hacer un juego de sábanas para nuestra cama?
- ¿Cuántos litros bastan para dar 3 manos de pintura al salón de conferencias?
- ¿Cuanta semilla alcanza para replantar todo el césped del jardín?
- ¿Cuántos camiones necesitaremos para acarrear la tierra obtenida al sacar una capa de 10 cm de todo el patio?
- ¿Qué productividad tiene la tierra agraria de una zona?
- ¿Qué tamaño de departamento necesitamos para satisfacer bien nuestras necesidades familiares de espacio?
- ¿Qué extensión tiene la cuenca del río Paraná?
Para contestar cualquiera de estas preguntas, y muchas otras, necesitamos comprender y saber calcular áreas. Se trata, en todos los casos, de cuantificaciones de superficies en relación con otras magnitudes muy variadas.
Origen histórico del concepto de área
A diferencia de las leyes físicas, químicas y biológicas, los conceptos matemáticos no son parte de la naturaleza sino provienen de la interacción de la mente humana con ella. Reflejan la manera en que está estructurado el pensamiento, sus elementos constitutivos, las relaciones entre ellos y las operaciones de transformación de ambos (estructuras y procesos mentales). Durante el proceso de evolución biológica de la especie humana estas características se adaptaron a la mejor resolución de sus problemas prácticos. Es por esta razón que la valoración y el rescate de la intuición del estudiante —experiencia internalizada no consciente, véase el artículo sobre saber— le facilita asumir el protagonismo activo de su propio aprendizaje, en vez de ser un desganado memorista que sólo busca satisfacer los aparentemente arbitrarios requerimientos de un maestro o profesor. Ésto es justamente lo que pasa cuando el concepto de área se desarrolla a partir de la aparentemente antojadiza definición de la de un cuadrado o rectángulo.
El concepto de área no es innato sino culturalmente transmitido. Se originó probablemente en tiempos prehistóricos cuando la especie humana era todavía nómade y vivía de la caza, la pesca y la recolección de frutos y raíces. La búsqueda de alimentos requería grandes recorridos en busca de las plantas y animales esenciales para la supervivencia. Al mismo tiempo, la competencia con otros grupos humanos requería respetar territorios ajenos o combatir por ellos, siendo el concepto de territorio afín al de área. En esta acepción operativa un área es una franja de territorio que se puede recorrer en cierto tiempo, dependiendo de la naturaleza del terreno y de la velocidad de desplazamiento. Este mismo concepto de área es el que tiene hoy aplicación práctica en un scanner, dispositivo electrónico que explora las características gráficas de una superficie por desplazamiento sobre ella, cuya correcta denominación castellana debería ser explorador por barrido.
La segunda acepción operativa de área —más básica, la usada en las ingenierías y en la Física— es la de cubrimiento y requiere un área de referencia como una manta, una alfombra o una baldosa. Esta acepción seguramente surgió en la etapa sedentaria de los asentamientos humanos estables, de la construcción de viviendas permanentes y de la ocupación continua de terrenos agrícolas y ganaderos. Por ejemplo, no se puede fabricar la cantidad de tela necesaria para vestir a una persona si no se tiene alguna manera de medir o calcular áreas. En esta acepción dos superficies cualesquiera (la del cuerpo y la de la tela, en el ejemplo anterior) tienen la misma área cuando una es capaz de cubrir a la otra sin sobrantes ni faltantes apreciables. Esta acepción, más simple, puede servir de fundamento a la primera acepción discutida, la del recorrido, que puede entonces considerarse como un proceso de cubrimiento virtual.
Áreas de figuras irregulares
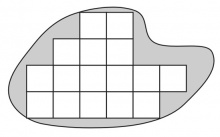
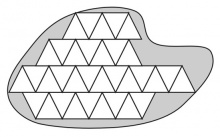
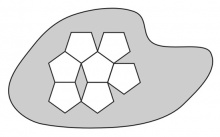
El concepto de cubrimiento se cuantifica cuando se usa una superficie de referencia (unidad) capaz de cubrir, por repetición, otra mucho mayor. Aquí es crítica la forma de la unidad para que sea capaz de cubrir áreas crecientes, por repetición y sin dejar huecos entre sí. Hay muchas formas con esa propiedad, siendo las más conocidas —por su uso en baldosas y azulejos— los cuadrados (véase la Figura 1) y rectángulos. Otras menos comunes son el triángulo equilátero, como se ilustra en la Figura 2, los paralelogramos de cualquier forma y los exágonos regulares. Es imposible, en cambio, cubrir una superficie con pentágonos regulares sin dejar huecos entre ellos (véase la Figura 3). Es importante aquí establecer bien la diferencia entre la ausencia de huecos y solapamientos entre piezas contiguas y la capacidad de cubrir cualquier forma sin excesos ni sobrantes, tema que se discute detalladamente a continuación.
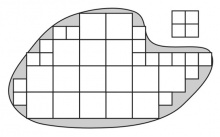
El grado de cubrimiento de figuras irregulares es mayor cuanto menor sea la unidad de área (el área de referencia). Para ello hay que subdivir esta área en fracciones, que en el caso de la Figura 4 son 1/4 de la unidad original para facilitar su visualización (la norma decimal es subdividir la unidad principal en décimas, centésimas, y así siguiendo). Si siguierámos subdiviendo aún más la unidad, lograríamos aproximarnos cada vez más a un cubrimiento completo, hasta el punto en que el error cometido fuera despreciable. El uso sucesivo de unidades cada vez más pequeñas hasta lograr el cubrimiento completo es la base del concepto matemático de área que se discute al final. El cubrimiento aproximado puede hacerse tanto por defecto (caso de la Figura 4) como por exceso (véase la Figura 8).
Elección de unidades de área
El cubrimiento permite determinar la igualdad de áreas, con un margen de error que depende de cual sea la menor fracción de la unidad de cubrimiento que se esté dispuesto a usar. En todo el análisis previo esta unidad era elegida arbitrariamente; podía ser una hoja de papel, un trozo de tela, una alfombra o cualquier otro objeto adaptable a la superficie cuya área se quiere determinar por comparación. Esta arbitrariedad —común a las unidades de cualquier magnitud, tales como una longitud, un tiempo o una luminosidad— crea problemas cuando se quiere comunicar áreas a alguien que no tiene acceso directo a la unidad. Por ejemplo, si alguien nos ofrece en EEUU un terreno cuya área es de 200 acres (unidad habitualmente usada en ese país), no sabremos de qué nos está hablando hasta que sepamos cómo compararla con nuestra unidad habitual para ese fin, la hectárea (ha).
La unidad adoptada universalmente por la Física (Sistema Internacional de unidades, o SI) es el área de un cuadrado de 1 metro de lado, o metro cuadrado (m², véase M). Para grandes áreas la operación de cubrimiento se facilita si se toman múltiplos de la unidad principal. Nótese, por ejemplo, que la zona central de la Figura 4 puede cubrirse con una super-unidad cuadrada formada por 9 unidades principales. Cada unidad convencional tiene un rango práctico de aplicación: el cm² para superficies que caben en nuestras manos, el m² para departamentos, la hectárea (1 ha=10.000 m²) para lotes y el km² (100 ha) para las áreas de provincias y países.
Áreas de figuras regulares
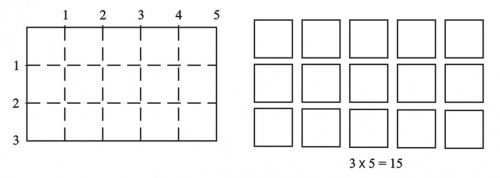
Las figuras más simples que se pueden recubrir de modo perfecto son los rectángulos cuyos lados son múltiplos enteros del lado de la unidad cuadrada de área (múltiplo o submúltiplo del m²). El rectángulo de la Figura 5, cuyos lados miden respectivamente 3 y 5 unidades de longitud (los segmentos indicados), se puede cubrir completamente con cuadraditos cuyos lados miden 1 unidad de longitud, y cuyo número, como se ve a simple vista, es el producto de las medidas de los lados. Para mayor claridad del argumento estos rectángulos se representan separados a la derecha de la figura. Esta propiedad es completamente general y conduce a la fórmula del área de un rectángulo como el producto de su base por su altura. No es una definición inventada sino una consecuencia del concepto de área como medida del cubrimiento. La definición es válida también para lados que no son múltiplos enteros, sino cualquier fracción del lado del cuadrado unidad de área. Se puede verificar que esto es cierto usando como nueva unidad de área un cuadradito cuyo lado es también una fracción similar del original.
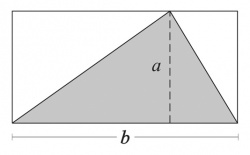
Con este modo de introducir el concepto de área es fácil comparar el área de un triángulo con la de un rectángulo. En la Figura 6 se muestra la manera habitual de hacer esta reducción mediante la subdivisión de un triángulo escaleno, operación válida también para los triángulos equiláteros, isósceles y rectángulos (el caso más simple). Se traza la altura a del triángulo grisado, la línea de trazos, subdividiéndolo en dos triángulos rectángulos menores. Se construyen dos triángulos iguales a éstos, ubicándolos de modo de formar un rectángulo. Este rectángulo tiene un área doble que la del triángulo, porque para cubrirlo se requieren dos triángulos como el original. El área A del triángulo es, entonces, igual a la mitad de la del rectángulo así construido, la mitad del producto de su altura a por su base b: A=a·b/2.
Cuando el concepto de área se introduce, como es habitual, definiendo a la de un rectángulo como el producto de su altura por su base, el método gráfico de cálculo del área de un triángulo aparece como un artificio injustificado, cuando en realidad no es así. El problema surge porque se empieza con una fórmula, no con un concepto. Toda fórmula es la expresión matemática de un concepto cuya formación debe alcanzarse primero. El origen de este tradicional encaramiento probablemente proviene de que las definiciones operativas, como la de cubrimiento, son parte natural de la Física y las ingenierías, pero no de la Matemática. En ésta el método seguro no es el uso de la intuición sino la introducción de postulados, siendo la definición de área uno de ellos.
Todos los polígonos pueden reducirse a triángulos, por lo que su área se calcula por cubrimiento con triángulos apropiados, cuya área se conoce a partir de las medidas de sus bases (lados) y alturas (apotemas). Aunque aparentemente no puede calcularse de esta forma el área de un círculo, en realidad no es así. Este problema, que se encara a continuación, permitirá comprender mejor la idea de cubrimiento completo que se planteó al comienzo.
El área de un círculo y el concepto de límite
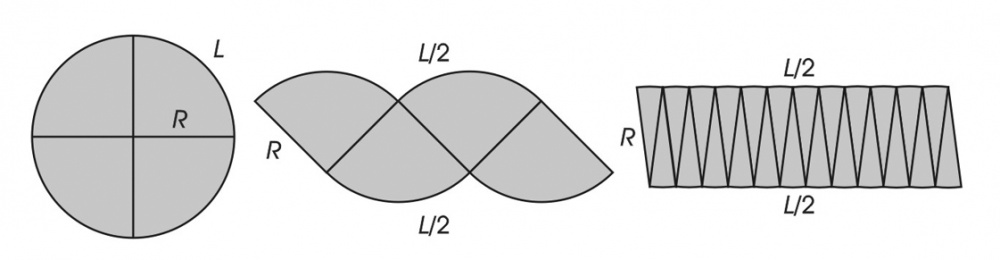
Los matemáticos han desarrollado un método muy general para calcular el área encerrada por curvas cerradas expresables mediante funciones matemáticas. La más regular de todas estas curvas, en el sentido de que tiene la mayor cantidad de simetrías, es la circunferencia. El área de la superficie plana encerrada por una circunferencia (el círculo) se puede calcular cubriéndola con sectores circulares que pueden reordenarse para asemejarse a un rectángulo. Comenzamos, para aclarar ideas, con su cubrimiento con sólo 4 sectores circulares y luego dividimos cada uno de estos por 6 llevándolos a 24, como se muestra en la Figura 7.
El cubrimiento es siempre perfecto cualquiera sea el número de sectores circulares usados, a diferencia de lo que sucedía en la Figura 4. La razón de aumentar su número es poder calcular su medida usando la fórmula básica del rectángulo. En efecto, cuanto más chicos son los sectores circulares más rectos se hacen los bordes y más tiende el “paralelogramo” a un rectángulo. Como usamos la mitad de los bordes externos de los sectores para formar el lado superior y la otra mitad para formar el inferior, su longitud es la misma e igual a la mitad del perímetro L de la circunferencia. Los lados “verticales” opuestos, por su parte, tienen longitudes iguales al radio R de la circunferencia. Por lo tanto, cuando los sectores circulares se hacen muy muy pequeños, la figura tiende a un rectángulo cuya área A vale
.
La relación entre el perímetro L y el radio R de la circunferencia es donde p = 3,14159... Reemplazando este valor de L en la fórmula del área se obtiene el conocido valor .
El antedicho proceso de cubrimiento conduce al mismo resultado que la inscripción o circunscripción en la circunferencia de polígonos regulares con cantidad creciente de lados. El centro y los vértices del polígono determinan triángulos isósceles la longitud de cuya base se hace infinitesimal (tiende a cero). Este método general de calcular un área cualquiera usando elementos de cubrimiento cada vez menores, el pasaje al límite infinitesimal, ya fue usado por los geómetras griegos hace más de 2.000 años. El uso de elementos de área infinitesimales es el punto de partida del cálculo integral inventado por Isaac Newton y Gottfried Leibniz hace casi 4 siglos, base imprescindible de la Física y las ingenierías actuales.
[[Archivo:|300px||thumb|Figura 8. Octógono inscripto y circunscripto en una circunferencia. El área gris corresponde al defecto y la negra al exceso de cubrimiento.
Del cubrimiento al concepto de integral
El cálculo de áreas mediante la operación matemática de integración se estudia en las escuela industriales argentinas en la asignatura Análisis Matemático. Una de las principales razones por las que los estudiantes tienen grandes dificultades para aprehenderlo en este nivel, al igual que en la universidad, es porque su concepto de área no ha sido introducido desde el punto de vista del cubrimiento.
En este método el número de áreas que se suman tiende a infinito y su tamaño tiende a cero. Es contrario a nuestra intuición el que la suma de infinitos elementos pueda dar un resultado finito. Es por eso conveniente, antes de iniciar el tratamiento de las integrales, ejemplificar primero cómo puede suceder tal cosa. Tomamos para ello un cuadrado de área A y lo dividimos por la mitad para obtener un rectángulo de área A/2. Luego dividimos en dos el rectángulo para obtener un cuadrado de área A/4. El proceso de subdivisión se continúa obteniendo alternadamente rectángulos y cuadrados cuyas áreas son siempre la mitad de las precedentes. La Figura 9 ilustra cómo la suma de las áreas de las infinitas figuras así obtenidas, que son cada vez más pequeñas, da un resultado finito que en este caso es exactamente A. En efecto, el área no cubierta de la esquina superior derecha se reduce a la mitad en cada paso, tendiendo a 0 a medida que se siguen agregando figuras. En tan sólo 10 pasos el área sin cubrir es menor que un milésimo del área A.
[[Archivo:|300px||thumb|Esta secuencia corresponde a la serie geométrica
Para definir con total precisión el área delimitada por una curva es necesario dar primero la descripción matemática de dicha curva a través del concepto de función y hacer su representación numérica en un sistema de coordenadas apropiado.
En el sistema de coordenadas cartesianas de la Figura 10 la curva superior está definida por la función y(x), cuyos valores para las abscisas indicadas es yn = y(xn). Las unidades elementales elegidas para cubrir el área comprendida entre la curva superior y el eje x son rectángulos de base constante Dx y altura variable yn. Estos rectángulos tienen lados paralelos a los ejes coordenados x e y, y están asentados sobre el eje horizontal x. El área A6 resultante del proceso de hacer tender a 0 el ancho de los rectángulos y a infinito su número, es la integral siguiente:
[[Archivo:|300px||thumb|El símbolo representa la operación de suma. El símbolo dx, introducido por Leibniz, indica el pasaje de Dx al límite infinitesimal. El cálculo integral, aparentemente muy complicado, se reduce luego a una operación mucho más fácil de calcular, la derivación, tema que no se discutirá aquí ni las múltiples aplicaciones que el concepto tiene en muy variados campos del saber.
Pareciera que el método no es apropiado para evaluar áreas de superficies cerradas arbitrarias, pero no es así. El uso de coordenadas cartesianas requiere descomponer el borde de la superficie (la curva y(x)) en segmentos de modo tal que el área deseada pueda obtenerse por diferencia. Como la explicación escrita es más complicada que la visual, remito al lector a la Figura 11 donde el área A deseada es la diferencia A1 – A2.
[[Archivo:|300px||thumb|También es posible y frecuente el uso de elementos de área de forma muy variada, como los sectores circulares usados en las integrales polares que se muestran en la Figura 11. Estos sectores están determinados por su radio rn, el ángulo polar qn que éste determina con el eje horizontal y su apertura Dq, constante para todos ellos. Si la curva es una circunferencia y se elige el origen de coordenadas en su centro, el método se reduce al de la Figura 7. Este método es generalizable a sistemas de coordenadas muy variados que por regla general no se estudian en los cursos normales de Física e ingenierías.
[[Archivo:|300px||thumb|Sin embargo, las antedichas integrales simples dan rigor matemático a un cubrimiento diferente del descripto en la Figura 4. El proceso de cubrimiento completo allí esbozado tiene su realización matemática rigurosa recién cuando se introducen las integrales dobles que describen la suma de cuadraditos de lados Dx y Dy cuyas longitudes tienden a cero. La diferencia con el proceso descripto por la Figura 10 es que en este último caso no se usan cuadraditos sino rectángulos cuyo ancho Dx se hace tender a cero, pero cuya altura Dy es finita. Las integrales dobles que corresponden al proceso de subdivisión representado en la Figura 12 son
El tercero y cuarto miembro de esta ecuación describen cómo estas integrales dobles se reducen a una sucesión de dos integrales simples. Cuando la curva que delimita la superficie es suficientemente “regular” (concepto que requiere una especificación compleja) esta reducción puede hacerse en cualquiera de los dos órdenes indicados.
El cálculo de áreas mediante integrales dobles puede hacer también en sistemas de coordenadas no cartesianas, como el de la Figura 11, pero este proceso no aporta conceptualmente nada nuevo.
Conclusiones
El concepto de área no surgió por capricho o vuelo de la imaginación sino por las necesidades prácticas de cuantificar cubrimientos de muy variado tipo, entre las que hoy podemos incluir algunas tridimensionales como las necesarias para la pintura de superficies no planas (caso de una cúpula). Ésto condujo naturalmente a la introducción de una unidad de superficie y de múltiplos y submúltiplos más apropiados para escalas mayores o menores que la original. La medida resultante (cantidad de unidades de referencia) es fácil de calcular cuando la unidad de cubrimiento es una forma regular simple como el rectángulo. Ésto no impide —de hecho es necesario en casos como el del círculo— el uso de unidades de cubrimiento de formas muy variadas cuya área, sin embargo, sigue calculándose en términos de cuadrados de tamaño apropiado (cm2, m2, ha = hm2, km2...). Trabajar el concepto de área sólo para figuras regulares puede ayudar a desarrollar el concepto de medida, pero no basta para las aplicaciones prácticas, las únicas que motivan el uso del concepto. Es por ello necesario desarrollar la noción de cubrimiento desde el mismo comienzo de su estudio.
Cuando se tiene una superficie que no puede cubrirse de manera exacta con triángulos, para obtener un cubrimiento (medida) perfecto es necesario recurrir a subunidades cada vez más pequeñas. La necesidad del pasaje al límite no es, por lo tanto, un artificio para la definición de integrales matemáticas sino un producto de la necesidad de hacer cubrimientos perfectos de superficies irregulares. Aunque desde el punto de vista práctico la precisión total no interesa, la Matemática la requiere de modo ineludible por razones que no es posible discutir aquí. Cuando se ilustra de modo apropiado, el concepto de pasaje al límite no es tan difícil como habitualmente se cree, aunque si lo es su definición matemática rigurosa. Este concepto es imprescindible para el tratamiento matemático de cualquier tecnología compleja y debería ser trabajado, en etapas apropiadas, en las escuelas primarias (para la que el esbozo dado en la primera parte de este trabajo es suficiente) y secundarias (donde hay que desarrollar temas adicionales).
La construcción del concepto de área, desde su origen intuitivo en operaciones de cubrimiento hasta su rigurosa formulación matemática, requiere (como todos los saberes complejos) transitar un largo camino. La mente humana construye las estructuras complejas en etapas y niveles de agregación. La identificación de esas etapas, su jerarquización y la manera de construir estructuras mentales donde los conceptos más complejos están basados en la organización de otros más simples en estructuras de inclusión como las de las muñequitas rusas mamuschkas, son requisitos esenciales para el buen trabajo docente. Como para el recorrido de cualquier trayecto, no sólo hay que saber el punto de partida sino también el de llegada, aunque no todos lo completen llegando, como en este caso, al concepto de integral matemática.
Fuentes
- Jean Piaget (compilador), La explicación en las ciencias (Coloquio de la Academia Internacional de Filosofía de las Ciencias, Ginebra, 1970), Ediciones Martínez Roca, Barcelona (España), 1977. En especial el capítulo 13.
- Richard Courant y Herbert Robbins, Qué es la Matemática, Editorial Alda, Buenos Aires (Argentina), 1954, pp. 441-446.
- J. Rey Pastor, P. Pi Calleja y C. A. Trejo, Análisis Matemático, vol. 1, Editorial Kapelusz, Buenos Aires (Argentina), 1952, cap. XIII.
- William Anthony Granville, Cálculo diferencial e integral, UTEHA, México, 1956, pp. 629?630.
- Julius Adams Stratton, Electromagnetic theory, McGraw Hill, New York (EE. UU.), 1941, pp. 47?59.
- Granville, op. cit., pp. 610?613.
- Felix Klein, Elementary Mathematics from an advanced standpoint: Arithmetic – Algebra – Analysis, Dover, New York (EE. UU.), pp. 211?220.
- Se discute detalladamente el concepto de estructura y su uso en la enseñanza en el trabajo Desarrollo de software educativo mediante síntesis sistémica: escritura electrónica.