Diferencia entre revisiones de «Cómo trazar una elipse»
La enciclopedia de ciencias y tecnologías en Argentina
m |
(lugar geométrico) |
||
| Línea 13: | Línea 13: | ||
==Elipse como lugar geométrico== | ==Elipse como lugar geométrico== | ||
| − | < | + | [[Archivo:Elipse lugar geométrico.jpg|150px|left|thumb|<small><center>'''Figura 2. La elipse como lugar geométrico.'''</center></small>]] |
| + | El concepto matematico de ''lugar geométrico'' puede "traducirse" al lenguaje cotidiano como ''curva determinada por una condición''. La definición matemática de una elipse como lugar geométrico se expresa así: | ||
| − | :La elipse es lugar geométrico de | + | :La elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a 2 puntos fijos (los focos) es constante. |
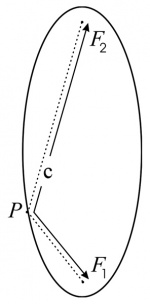
| + | En la Figura 2 se muestra como construir una elipse a partir de sus focos, indicados con F<sub>1</sub> y F<sub>2</sub>. El concepto de foco tiene importantes aplicaciones científicas. Por ejemplo, el sol está ubicado en uno de sus foco de la elipse que traza la Tierra al girar a su alrededor. | ||
| + | <!-- | ||
| + | Se puede relacionar la altura y ancho de la elipse con sus parámetros matemáticos usando la siguiente definición: | ||
La definición se ilustra en la Figura 2, donde la suma de las distancia del punto P de la elipse a los dos focos es la suma de las longitudes de segmentos F1P + PF2 = l, donde l vale lo mismo para cualquier otro punto de la elipse. El método constructivo basado en esta definición consiste en clavar en una base dos clavitos en la posición de los focos y fijar a ellos un trozo de piolín. Con la punta de un lápiz se tensa el piolín y se trazan sobre la base los puntos de la elipse. | La definición se ilustra en la Figura 2, donde la suma de las distancia del punto P de la elipse a los dos focos es la suma de las longitudes de segmentos F1P + PF2 = l, donde l vale lo mismo para cualquier otro punto de la elipse. El método constructivo basado en esta definición consiste en clavar en una base dos clavitos en la posición de los focos y fijar a ellos un trozo de piolín. Con la punta de un lápiz se tensa el piolín y se trazan sobre la base los puntos de la elipse. | ||
Revisión del 22:10 1 nov 2011
Cómo trazar una elipse describe una técnica simple para trazar una elipse de dimensiones prefijadas. Por su simplicidad puede usarse para hacer el marco de una fotografía, el tablero de una mesa o el trazado de un cantero de forma elipsoidal en jardinería (campo en que el método es conocido desde hace mucho tiempo). La técnica ilustra también que la definición de una curva como un lugar geométrico facilita el desarrollo de un método práctico de trazado sin hacer uso de coordenadas cartesianas —la manera usual, pero más compleja.
El problema
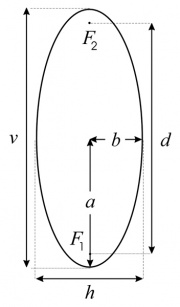
El problema práctico aparece al querer trazar "óvalos", como los bordes de un portarretratos, donde las dimensiones requeridas son la altura v (la mayor dimensión en el caso de un retrato) y el ancho h (la menor, véase la Figura 1). Los óvalos, especie de circunferencias achatadas, no son curvas matemáticamente bien definidas, ya que hay varias con este rasgo que no pueden diferenciarse unas de otras a simple vista. Aunque esta indeterminación no tiene importancia para el lego en Matemática, el desarrollo de una técnica de trazado requiere optar por una sola familia de curvas. Se eligen aquí las elipses, curvas que se obtiene al seccionar un cono con un plano y que también son las trayectorias que describen los planetas alrededor del sol.
Como se ilustra en la Figura 1, la forma de una elipse cualquiera queda completamente determinada por 2 longitudes diferentes denominadas sus semiejes. En la Figura 1 el semieje mayor es la longitud del segmento a y el semieje menor la del segmento b. Uno de los rasgos especiales que tienen las elipses es que cuando sus 2 semiejes son iguales se obtiene una circunferencia. Se ve fácilmente en la figura que la altura v y el ancho h de la elipse valen
- v = 2a, h = 2b. (Ecuación 1).
La Figura 1 contiene otros datos que serán necesarios para el trazado de la elipse. Para ello es necesario caracterizar la curva de manera matemáticamente precisa, lo que se hace a continuación.
Elipse como lugar geométrico
El concepto matematico de lugar geométrico puede "traducirse" al lenguaje cotidiano como curva determinada por una condición. La definición matemática de una elipse como lugar geométrico se expresa así:
- La elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a 2 puntos fijos (los focos) es constante.
En la Figura 2 se muestra como construir una elipse a partir de sus focos, indicados con F1 y F2. El concepto de foco tiene importantes aplicaciones científicas. Por ejemplo, el sol está ubicado en uno de sus foco de la elipse que traza la Tierra al girar a su alrededor.