Diferencia entre revisiones de «Cómo trazar una elipse»
La enciclopedia de ciencias y tecnologías en Argentina
(fin texto, faltan Figuras 4 y 5) |
m |
||
| Línea 44: | Línea 44: | ||
La Ecuación 4 establece que la longitud ''c'' del cordel usado para el trazado debe ser igual a la altura ''v'' deseada para la elipse. | La Ecuación 4 establece que la longitud ''c'' del cordel usado para el trazado debe ser igual a la altura ''v'' deseada para la elipse. | ||
| − | La separación ''d'' de los focos, la longitud ''F''<sub>1''F''<sub>2</sub> se obtiene de la Figura 5, donde el punto ''S'' de la elipse está sobre la recta que contiene al semieje menor ''b''. Esta recta divide al triángulo isósceles de vértices F''<sub>1</sub>, F''<sub>2</sub> y ''S'', en dos triángulos rectángulos congruentes. Las longitudes de los 3 lados de cualquiera de estos triángulos, por ejemplo el F''<sub>1</sub>''OS'', cumplen el Teorema de Pitágoras: | + | La separación ''d'' de los focos, la longitud ''F''<sub>1</sub>''F''<sub>2</sub> se obtiene de la Figura 5, donde el punto ''S'' de la elipse está sobre la recta que contiene al semieje menor ''b''. Esta recta divide al triángulo isósceles de vértices F''<sub>1</sub>, F''<sub>2</sub> y ''S'', en dos triángulos rectángulos congruentes. Las longitudes de los 3 lados de cualquiera de estos triángulos, por ejemplo el ''F''<sub>1</sub>''OS'', cumplen el Teorema de Pitágoras: |
| − | : ''SO''² + ''OF''<sub>1</sub>² = F''<sub>1</sub>''S''² | + | : ''SO''² + ''OF''<sub>1</sub>² = ''F''<sub>1</sub>''S''² |
donde | donde | ||
| − | :''SO'' = ''h | + | :''SO'' = ''h''/2, ''OF''<sub>1</sub> = ''d''/2 y ''F''<sub>1</sub>''S'' = ''c''/2. |
| − | ''/2, ''OF''<sub>1</sub> = ''d''/2 y F''<sub>1</sub>''S' = ''c''/2. | ||
Simplificando los denominadores, resulta | Simplificando los denominadores, resulta | ||
| Línea 61: | Línea 60: | ||
:''d'' = √(''c''² - ''h''²) (Ecuación 5). | :''d'' = √(''c''² - ''h''²) (Ecuación 5). | ||
| − | La Ecuación 5 establece que para trazar una elipse de ancho ''h'', cuando se usa una longitud ''c'' de cordel, hay que separar los soportes del cordel (clavos o estacas) en la distancia dada por esa | + | La Ecuación 5 establece que para trazar una elipse de ancho ''h'', cuando se usa una longitud ''c'' de cordel, hay que separar los soportes del cordel (clavos o estacas) en la distancia dada por esa raíz cuadrada. |
==Ejemplo simple== | ==Ejemplo simple== | ||
| − | Por ejemplo, para construir | + | Por ejemplo, para construir una elipse de altura ''v'' = 15 cm y ancho ''h'' = 12 cm, la longitud del piolín debe ser ''c'' = 15 cm y la separación entre clavitos ''d'' = 9 cm. |
==Ecuación de las elipses en coordenadas cartesianas ortogonales== | ==Ecuación de las elipses en coordenadas cartesianas ortogonales== | ||
Revisión del 21:08 2 nov 2011
Cómo trazar una elipse describe una técnica simple para trazar una elipse de dimensiones prefijadas. Por su simplicidad puede usarse para hacer el marco de una fotografía, el tablero de una mesa o el trazado de un cantero de forma elipsoidal en jardinería (campo en que el método es conocido desde hace mucho tiempo). La técnica ilustra también que la definición de una curva como lugar geométrico facilita el desarrollo de un método práctico de trazado sin hacer uso de coordenadas cartesianas —la manera usual, pero más compleja.
Contenido
El problema
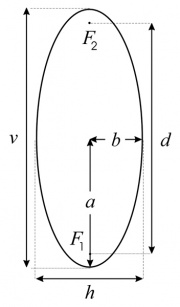
El problema práctico aparece al querer trazar "óvalos", como los bordes de un portarretratos, donde las dimensiones requeridas son la altura v (la mayor dimensión en el caso de un retrato) y el ancho h (la menor, véase la Figura 1). Los óvalos, especie de circunferencias achatadas, no son curvas matemáticamente bien definidas, ya que hay varias con este rasgo que no pueden diferenciarse unas de otras a simple vista. Aunque esta indeterminación no tiene importancia para el lego en Matemática, el desarrollo de una técnica de trazado requiere optar por una sola familia de curvas. Se eligen aquí las elipses, curvas que se obtiene al seccionar un cono con un plano y que también son las trayectorias que describen los planetas alrededor del sol.
Como se ilustra en la Figura 1, la forma de una elipse cualquiera queda completamente determinada por 2 longitudes diferentes denominadas sus semiejes. En la Figura 1 el semieje mayor es la longitud del segmento a y el semieje menor la del segmento b. Un rasgo característico de las elipses es que cuando sus 2 semiejes son iguales se obtiene una circunferencia. Se ve fácilmente en la figura que la altura v y el ancho h de la elipse valen
- v = 2a, h = 2b. (Ecuación 1).
La Figura 1 contiene otros datos que serán necesarios para el trazado de la elipse cuando se caracterice la curva de manera matemáticamente precisa.
Elipse como lugar geométrico
El concepto matematico de lugar geométrico puede "traducirse" al lenguaje cotidiano como curva determinada por una condición. La definición matemática de una elipse como lugar geométrico se expresa así:
- La elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a 2 puntos fijos, sus focos, es constante.
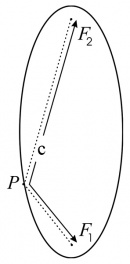
En la Figura 2 se individualizan los focos con los símbolos F1 y F2 y las distancias del punto P a cada uno ellos. El concepto de foco tiene importantes aplicaciones científicas: por ejemplo, el sol está ubicado en uno de los foco de la elipse que traza la Tierra cuando gira a su alrededor. En la figura, la suma c de las distancias del punto P a los 2 focos es la siguiente suma de longitudes de segmentos:
- F1P + PF2 = c (Ecuación 2).
Esta suma tiene el mismo valor para cualquier punto P; es decir, c es una longitud fija (una constante) característica de una elipse dada. También es una constante la distancia d entre sus focos. Ambas constantes, c y d, definen completamente una única elipse.
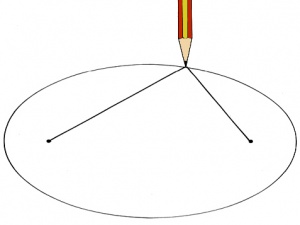
Esta definición de elipse permite su trazado de modo muy simple. La constancia de la longitud c se obtiene con un cordel no elástico: una gomilla no serviría ya que puede variar su longitud al estirarse y contraerse. La posición de los 2 focos se obtiene con clavos fijados a una madera o estacas fijadas al suelo, según el tipo de forma elíptica a construir. La curva se obtiene deslizando un trazador (lápiz, tiza, palo...) a lo largo del cordel, cuyos extremos deben estar fijos a un par de clavos o estacas. El método se ilustra en la Figura 3.
Solo falta relacionar entre sí los 2 pares de datos requeridos para este trazado: la longitud c del cordel y la distancia d entre los focos con la altura v y el ancho h deseados para la elipse.
Relaciones entre v, h, c y d
Las relaciones entre v, h, c y d se pueden encontrar usando la definición de la elipse como lugar geométrico. En la Figura 4 se muestra que para los puntos Q y R ubicados sobre la recta que contiene al semieje mayor a de la elipse (definido en la Figura 1), se cumple la siguiente igualdad de longitudes de segmentos:
- F1Q + QF2 = c (Ecuación 3).
Por la simetría de la elipse, son iguales las longitudes de los siguientes segmentos:
- QF2 = RF1,
que reemplazado en el primer miembro de la Ecuación 3 da
- F1Q + RF2 = v = c (Ecuación 4).
La Ecuación 4 establece que la longitud c del cordel usado para el trazado debe ser igual a la altura v deseada para la elipse.
La separación d de los focos, la longitud F1F2 se obtiene de la Figura 5, donde el punto S de la elipse está sobre la recta que contiene al semieje menor b. Esta recta divide al triángulo isósceles de vértices F1, F2 y S, en dos triángulos rectángulos congruentes. Las longitudes de los 3 lados de cualquiera de estos triángulos, por ejemplo el F1OS, cumplen el Teorema de Pitágoras:
- SO² + OF1² = F1S²
donde
- SO = h/2, OF1 = d/2 y F1S = c/2.
Simplificando los denominadores, resulta
- h² + d² = c², o sea, d² = c² - h².
Por lo tanto,
- d = √(c² - h²) (Ecuación 5).
La Ecuación 5 establece que para trazar una elipse de ancho h, cuando se usa una longitud c de cordel, hay que separar los soportes del cordel (clavos o estacas) en la distancia dada por esa raíz cuadrada.
Ejemplo simple
Por ejemplo, para construir una elipse de altura v = 15 cm y ancho h = 12 cm, la longitud del piolín debe ser c = 15 cm y la separación entre clavitos d = 9 cm.
Ecuación de las elipses en coordenadas cartesianas ortogonales
Aunque no es necesaria para la técnica de trazado, se incluye aquí la expresión matemática de las elipses. Si x es la abcisa e y la ordenada, en el sistema de coordenadas cartesianas ortogonales xy la ecuación de la elipse de semiejes a y b es:
- x²/a² + y²/b² = 1.
Fuentes
- Korn y Korn; Mathematical handbook for scientists and engineers; McGraw-Hill; Nueva York (EEUU); 1961; p. 50. Se dan ecuaciones que describen gran cantidad de propiedades de las elipses en sistemas de coordenadas cartesianas ortogonales.