Diferencia entre revisiones de «Torre de Brahma»
La enciclopedia de ciencias y tecnologías en Argentina
(16 etapas desplegadas) |
m |
||
| Línea 54: | Línea 54: | ||
<br> | <br> | ||
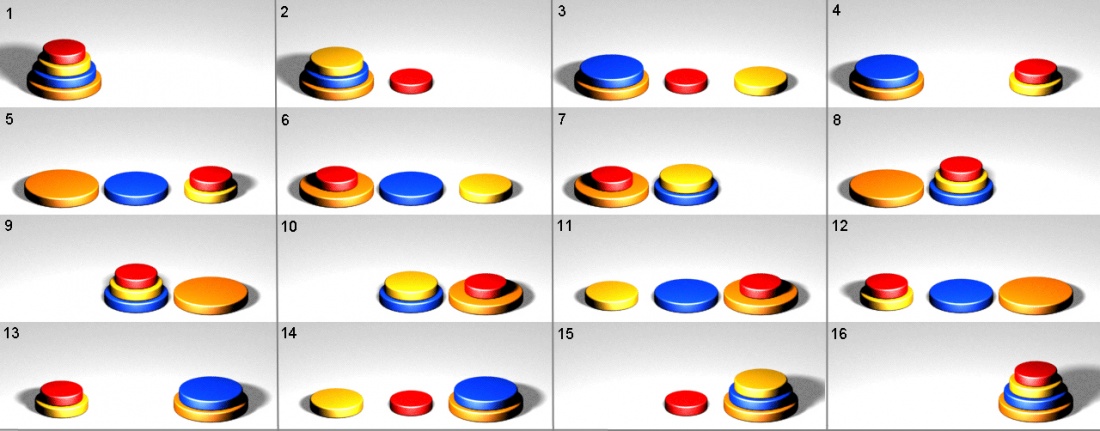
| − | [[Archivo:Torre de Brahma 4 discos 16 etapas.jpg| | + | [[Archivo:Torre de Brahma 4 discos 16 etapas.jpg|1100px|center|thumb|<small><center>'''16 etapas de la resolución de la Torre de Brahma de 4 discos.'''</center></small>]] |
===Informática=== | ===Informática=== | ||
Revisión del 18:25 8 dic 2013
La Torre de Brahma, también denominado Torre de Hanoi por razones desconocidas, es un juego de ingenio inventado por el matemático francés Édouard Lucas. Consiste en pasar una pila de discos perforados de tamaño decreciente de una varilla a otra, usando una varilla intermediaria. El juego tiene sólo dos reglas:
- sólo se puede pasar un disco por vez;
- sólo se puede poner un disco sobre otro de mayor diámetro.
El desafío es hacer la transferencia de los discos en el menor número de pases, que para n discos es 2n-1.
Contenido
Historia
El problema apareció en el tomo 3 del libro de Lucas Récréations mathématiques, publicado en 1892 después de su muerte. Con el título Les brahmes tombent (Los brahmanes colapsan), se atribuye allí la descripción del problema a un personaje ficticio, N. Claus de Siam (anagrama de Lucas d'Amiens, ya que Amiens era la ciudad natal del matemático), profesor del colegio Li-Sou-Stian (anagrama del liceo Saint Louis donde éste era profesor). El texto expresa:
- Durante los viajes hechos para la publicación de los escritos del ilustre Fer-Fer-Tam-Tam, N. Claus de Siam vio en el gran templo de Benarés, debajo de una cúpula que marca el centro del mundo, tres varillas de diamante embutidas en una base de bronce, de la altura de 1 codo [unos 45 cm] y el grosor del cuerpo de una abeja. Sobre una de las varillas Dios ensartó, en el comienzo de los tiempos, 64 discos de oro puro; el mayor de todos apoyado sobre el bronce y los demás, cada vez más pequeños, apilados hasta el final de la varilla. Es la torre sagrada de Brahma. Día y noche los sacerdotes se turnan sobre las gradas del altar para trasladar la torre de la primera varilla a la tercera, respetando las antedichas reglas impuestas por Brahma. Cuando se complete la tarea la torre y los brahmanes colapsarán y acaecerá el fin del mundo.
Benarés era el nombre dado por los europeos a la actual ciudad india de Varanasi, situada sobre la margen del río Ganges. Allí está el templo de Kashi Vishwanath, supuestamente creado por el dios Brahma para celebrar al dios Shiva, pero no hay allí varillas de diamante ni discos de oro, aunque el oro y la plata abundan en su decoración. Es incomprensible el nombre Torre de Hanoi dado posteriormente al juego —probablemente por alguna empresa que lo comercializó haciéndolo popular— porque Hanoi está en Vietnam, no en India.
La cantidad de pases necesarios para transferir los 64 discos citados a la tercer varilla es 18.446.744.073.709.551.615. Suponiendo que se haga un pase cada segundo, sin ninguna equivocación, y que la tarea se haga sin parar todos los días del año, se requerirían unos 585.000 millones de años para completarla, unas 40 veces la edad del universo.
Resolución
Algorítmica
Un algoritmo es una técnica de resolución de un problema matemático mediante una sucesión bien especificada de operaciones. Aunque todo algoritmo tiene una justificación matemática, no es necesario conocerla para aplicarlo. Tal es el caso, por ejemplo, de los algoritmos de multiplicación y división de números decimales, que funcionan bien aunque no sepamos su justificación.
La torre de Brahma se resuelve mediante un algoritmo muy simple que consta de sólo tres reglas. Para aplicarlo conviene distribuir las varillas o puntos de apoyo de los discos en forma de triángulo equilátero y diferenciar los discos de modo alternado, sea con colores o con alguna marca. Si se numeran los discos de menor a mayor, donde 1 es el menor de todos, 2 el que le sigue en orden creciente de tamaño y así sucesivamente, los discos identificados por números impares deben marcarse para diferenciarlos fácilmente de los pares (como en la figura adjunta, por ejemplo). Hecho ésto, el algoritmo de resolución —siempre respetando la regla del tamaño que prohibe colocar un disco sobre otro de menor diámetro— es el siguiente:
- Hay que mover siempre el disco 1 a la posición contigua en el sentido de rotación de las agujas del reloj (sentido horario, mirando desde arriba) y alternándolo con otro disco par o impar una de cada dos vueltas.
- El movimiento de otro disco diferente al más pequeño debe hacerse en la posición contigua del sentido horario si es impar o antihorario si es par.
- Si no puede colocarse un disco en la posición contigua sin violar la regla del tamaño, se usa la posición siguiente, siempre respetando el sentido de rotación que le corresponde por su paridad.
Alternativamente, se puede elegir para el disco 1 el sentido de rotación antihorario —cambiando de modo apropiado el resto de las reglas— sin que el algoritmo pierda eficacia. Si se respetan rigurosamente las nuevas reglas, está asegurada la resolución de la Torre de Brahma con el número mínimo de movimientos para cualquier número n de discos, lo que debe verificarse contándolos y comparando con el valor de 2n-1.
Matemática
La Torre de Brahma puede resolverse usando relaciones de recurrencia, un método importante en muchas ramas de la Matemática, en especial para la construcción de secuencias y el cálculo de series de números. La base de este método es que el traslado a otra varilla de cualquier número de discos puede descomponerse en una serie de traslados de números decrecientes de discos. El caso más simple que conviene resolver para ello es reducir el traslado de 4 discos al de 3 (véase la animación al tope de la página). Se descubre entonces que el número de pases necesarios para resolver el caso de 4 discos es el doble que para el de 3, más 1. En efecto, primero hay que llevar los 3 discos a otra varilla, dejando el 4º libre. Luego hay que trasladar éste a la varilla libre y, finalmente, reacomodar la pila de 3 discos sobre él.
Lo mismo sucede para el traslado de cualquier número n de discos, que se puede hacer mediante 2 traslados de n-1 discos, más 1. Si Tn es el número de pases requeridos para trasladar n discos, ésto se puede escribir así:
que es la relación de recurrencia buscada. Para n = 1 basta 1 pase, por lo que
Por la fórmula general se tiene entonces,
T3 = 2·T2 + 1 = 2·(22 -1) + 1 = 23 -1,
…
El juego también puede resolverse mediante la Teoría de Grafos o usando notación binaria (véase el artículo de Wikipedia en inglés). Aunque el tema no se discutirá aquí por requerir saberes matemáticos especializados, es importante señalar que la estructura del método de resolución es isomorfa (véase el artículo Uso de metáforas en la enseñanza) con la de resolución de problemas —aparentemente muy diferentes— de otros juegos y de la computación (véase Gardner).
Informática
El algoritmo que resuelve el problema de la Torre de Brahma puede programarse en cualquier lenguaje de computación, pero es especialmente simple en Prolog. La razón es que este lenguaje de inteligencia artificial está especialmente diseñado para —entre muchas otras características— operar con relaciones de recurrencia. En Visual Prolog®, por ejemplo, el problema se resuelve con sólo 2 cláusulas[1].
Construcción de una Torre de Brahma
El método más simple es cortar discos de un material grueso como goma EVA o cartón y usar una base triangular de papel con circunferencias guía para la colocación de las 3 pilas. El más caro y estético es hacer discos, base y varillas de madera, haciendo los discos de dos maderas nobles diferentes, alternando una clara con otra oscura.
Fuentes
- Tours de Hanoï en Wikipedia en francés.
- Tower of Hanoi en Wikipedia en inglés.
- Gardner, Martin; Mathematical Puzzles and Diversions; Penguin Books; Inglaterra (Reino Unido); 1959; pp. 56‑61.
- Tower of Hanoi, artículo de Wolfram MathWorld que contiene múltiples propiedades y referencias matemáticas sobre el juego.
- Endless Hanoi Tower, juego gratuito para iPod e iPhone. Hay otras aplicaciones para dispositivos móviles de las marcas líderes.
- Solivérez, Carlos E.; La Torre de Brahma; versión original de este artículo.