Diferencia entre revisiones de «Estructuras portantes»
La enciclopedia de ciencias y tecnologías en Argentina
m (Texto reemplaza - '—' a '—') |
m |
||
| Línea 21: | Línea 21: | ||
* puente dental, | * puente dental, | ||
* soporte, | * soporte, | ||
| − | |[[Archivo:Armadura techo.jpg|950px|center|thumb|<center>'''Figura 1. Armadura de un tejado.'''</center>]] | + | |[[Archivo:Armadura techo.jpg|950px|center|thumb|<small><center>'''Figura 1. Armadura de un tejado.'''</center></small>]] |
|} | |} | ||
| Línea 31: | Línea 31: | ||
==Construcción de estructuras portantes simples con sorbetes e hilos de coser== | ==Construcción de estructuras portantes simples con sorbetes e hilos de coser== | ||
| − | [[Archivo:Tetraedro pajitas.jpg|300px|right|thumb|<center>'''Figura 2. Construcción de un tetraedro con pajitas.'''</center>]] | + | [[Archivo:Tetraedro pajitas.jpg|300px|right|thumb|<small><center>'''Figura 2. Construcción de un tetraedro con pajitas.'''</center></small>]] |
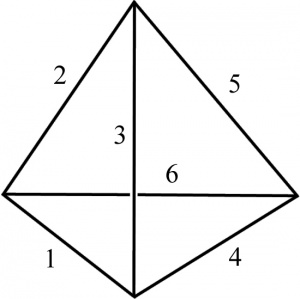
Se puede construir facilmente y sin costo tanto estructuras planas como tridimensionales usando canutillos para sorber gaseosas (en Argentina llamados ''pajitas'' o ''sorbetes'') e hilo común de coser. Para ello se pasan trozos de hilo suficientemente largos por el interior de sucesivas pajitas, anudándolos en vértices adecuados. Se ilustra el método con la construcción del tetraedro de la Figura 2. Se forma el primer triángulo pasando un hilo sucesivamente por el interior de los canutillos 1, 2 y 3 y anudando sus extremos. Se sujetan luego, de manera similar, los canutillos 4 y 5 al 3 del triángulo precedente, formando así dos triángulos articulados sobre el mismo eje (el lado 3). Se forma finalmente la base del tetraedro uniendo el canutillo 6 a los lados 2 y 5 (o 1 y 4) — pasando siempre el hilo a través de todos los canutillos involucrados. Es muy difícil pasar los hilos por el interior de las pajitas sin el auxilio de una herramienta apropiada. Es un valioso desafío plantear el diseño y construcción de la herramienta que permita hacerlo: un alambre fino (como los usados en las florerías) con un ojalillo en la punta. Esta parte de la actividad ilustra de modo concreto la necesidad y viabilidad de la fabricación de las propias herramientas de trabajo, destreza esencial para los artesanos. | Se puede construir facilmente y sin costo tanto estructuras planas como tridimensionales usando canutillos para sorber gaseosas (en Argentina llamados ''pajitas'' o ''sorbetes'') e hilo común de coser. Para ello se pasan trozos de hilo suficientemente largos por el interior de sucesivas pajitas, anudándolos en vértices adecuados. Se ilustra el método con la construcción del tetraedro de la Figura 2. Se forma el primer triángulo pasando un hilo sucesivamente por el interior de los canutillos 1, 2 y 3 y anudando sus extremos. Se sujetan luego, de manera similar, los canutillos 4 y 5 al 3 del triángulo precedente, formando así dos triángulos articulados sobre el mismo eje (el lado 3). Se forma finalmente la base del tetraedro uniendo el canutillo 6 a los lados 2 y 5 (o 1 y 4) — pasando siempre el hilo a través de todos los canutillos involucrados. Es muy difícil pasar los hilos por el interior de las pajitas sin el auxilio de una herramienta apropiada. Es un valioso desafío plantear el diseño y construcción de la herramienta que permita hacerlo: un alambre fino (como los usados en las florerías) con un ojalillo en la punta. Esta parte de la actividad ilustra de modo concreto la necesidad y viabilidad de la fabricación de las propias herramientas de trabajo, destreza esencial para los artesanos. | ||
| Línea 42: | Línea 42: | ||
# ¿Se les ocurre un método general para hacer totalmente estable un polígono construido con canutillos e hilos? | # ¿Se les ocurre un método general para hacer totalmente estable un polígono construido con canutillos e hilos? | ||
| − | [[Archivo:Puente ferroviario.jpg|300px|left|thumb|<center>'''Figura 3. Puente ferroviario.'''</center>]] | + | [[Archivo:Puente ferroviario.jpg|300px|left|thumb|<small><center>'''Figura 3. Puente ferroviario.'''</center></small>]] |
La respuesta al primer problema es obviamente la formación de subestructuras triangulares mediante el agregado de una diagonal. Como la longitud de una diagonal es mayor que la de un lado y los canutillos típicamente tienen la misma longitud, se requiere disminuir por recorte los lados del cuadrado. Para calcular la disminución hay que usar el Teorema de Pitágoras, problema de nivel secundario avanzado o terciario. Los más pequeños pueden encontrarlo por prueba y error, recortando paulatinamente los canutillos que forman los lados (todos a la vez para asegurar su igualdad) hasta que la longitud del no recortado coincida con la diagonal del cuadrado. La técnica de formación de triángulos para estabilizar estructuras portantes es muy frecuente y puede verse en todo tipo de estructuras de acero, de las cuales la más famosa es la torre Eiffel. Son ejemplos comunes los puentes ferroviarios como el que se ilustra en la Figura 3 y el apuntalamiento de los postes esquineros de cualquier alambrado rural, pero basta mirar con cuidado a nuestro alrededor, en cualquier lugar que estemos, para encontrar uno equivalente. Los soportes de un estante (ménsulas) son un ejemplo, busque otros. | La respuesta al primer problema es obviamente la formación de subestructuras triangulares mediante el agregado de una diagonal. Como la longitud de una diagonal es mayor que la de un lado y los canutillos típicamente tienen la misma longitud, se requiere disminuir por recorte los lados del cuadrado. Para calcular la disminución hay que usar el Teorema de Pitágoras, problema de nivel secundario avanzado o terciario. Los más pequeños pueden encontrarlo por prueba y error, recortando paulatinamente los canutillos que forman los lados (todos a la vez para asegurar su igualdad) hasta que la longitud del no recortado coincida con la diagonal del cuadrado. La técnica de formación de triángulos para estabilizar estructuras portantes es muy frecuente y puede verse en todo tipo de estructuras de acero, de las cuales la más famosa es la torre Eiffel. Son ejemplos comunes los puentes ferroviarios como el que se ilustra en la Figura 3 y el apuntalamiento de los postes esquineros de cualquier alambrado rural, pero basta mirar con cuidado a nuestro alrededor, en cualquier lugar que estemos, para encontrar uno equivalente. Los soportes de un estante (ménsulas) son un ejemplo, busque otros. | ||
| Línea 49: | Línea 49: | ||
==Explicación de la estabilidad de las estructuras portantes triangulares== | ==Explicación de la estabilidad de las estructuras portantes triangulares== | ||
| − | [[Archivo:Estabilidad triángulos.jpg|300px|right|thumb|<center>'''Figura 4. Construcción de un triángulo dados sus lados.'''</center>]] | + | [[Archivo:Estabilidad triángulos.jpg|300px|right|thumb|<small><center>'''Figura 4. Construcción de un triángulo dados sus lados.'''</center></small>]] |
Durante los más de 500.000 años de su evolución, a partir de las primeras herramientas de piedra, las tecnologías fueron descubiertas por azar y desarrolladas por [[ensayo y error]]. Es muy reciente la comprensión de que tan pronto se supera la etapa más rudimentaria estos métodos son ineficaces. Es necesario, por ello, crear en los educandos la conciencia de que las experiencias exclusivamente sensoriales y motrices, la experimentación, no es suficiente para el buen desarrollo de las tecnologías, se requiere también un análisis racional. Esto permitiría, si las hubiera, usar estructuras alternativas apropiadas al problema portante a resolver. Para ello se les plantea el siguiente problema: | Durante los más de 500.000 años de su evolución, a partir de las primeras herramientas de piedra, las tecnologías fueron descubiertas por azar y desarrolladas por [[ensayo y error]]. Es muy reciente la comprensión de que tan pronto se supera la etapa más rudimentaria estos métodos son ineficaces. Es necesario, por ello, crear en los educandos la conciencia de que las experiencias exclusivamente sensoriales y motrices, la experimentación, no es suficiente para el buen desarrollo de las tecnologías, se requiere también un análisis racional. Esto permitiría, si las hubiera, usar estructuras alternativas apropiadas al problema portante a resolver. Para ello se les plantea el siguiente problema: | ||
:La dificultad de deformación de un triángulo,¿proviene de propiedades geométricas del triángulo, de las propiedades físicas de los materiales con que está hecho o de una combinación de ambas? Justifiquen su respuesta de la manera más racional posible. | :La dificultad de deformación de un triángulo,¿proviene de propiedades geométricas del triángulo, de las propiedades físicas de los materiales con que está hecho o de una combinación de ambas? Justifiquen su respuesta de la manera más racional posible. | ||
| Línea 62: | Línea 62: | ||
==La cúpula geodésica== | ==La cúpula geodésica== | ||
| − | [[Archivo:Cúpula Epcot poligonada.jpg|300px|right|thumb|<center>'''Figura 5. Esfera geodésica de Epcot Center.'''</center>]] | + | [[Archivo:Cúpula Epcot poligonada.jpg|300px|right|thumb|<small><center>'''Figura 5. Esfera geodésica de Epcot Center.'''</center></small>]] |
La culminación de las estructuras portantes basadas en triángulos es la esfera o cúpula geodésica inventada por el arquitecto estadounidense [http://es.wikipedia.org/wiki/Buckminster_FullerRichard Buckminster Fuller] (1895-1983). Está basada en la estructura del icosaedro truncado inventado por el geómetra griego Arquímedes (287-212 aC), la forma de la pelota olímpica de fútbol (véase Ghyka). Las caras de este poliedro son exágonos y pentágonos cuyos ángulos interiores se estabilizan mediante pirámides triangulares. El resultado es una estructura extremadamente liviana y resistente, como la del Epcot Center que se muestra en la Figura 5. Se ha marcado allí, para mejor comprensión de la estructura, un pentágono y un exágono, ya que las pirámides triangulares son claramente visibles. | La culminación de las estructuras portantes basadas en triángulos es la esfera o cúpula geodésica inventada por el arquitecto estadounidense [http://es.wikipedia.org/wiki/Buckminster_FullerRichard Buckminster Fuller] (1895-1983). Está basada en la estructura del icosaedro truncado inventado por el geómetra griego Arquímedes (287-212 aC), la forma de la pelota olímpica de fútbol (véase Ghyka). Las caras de este poliedro son exágonos y pentágonos cuyos ángulos interiores se estabilizan mediante pirámides triangulares. El resultado es una estructura extremadamente liviana y resistente, como la del Epcot Center que se muestra en la Figura 5. Se ha marcado allí, para mejor comprensión de la estructura, un pentágono y un exágono, ya que las pirámides triangulares son claramente visibles. | ||
Revisión actual del 10:41 18 dic 2013
Se llama estructura portante a la que proporciona soporte a un edificio, en particular a su techo. Una estructura portante es una ilustración simple del concepto de estructura. En el presente artículo se propone una manera de promover la elaboración del concepto en la Educación Tecnológica.
Contenido
Introducción
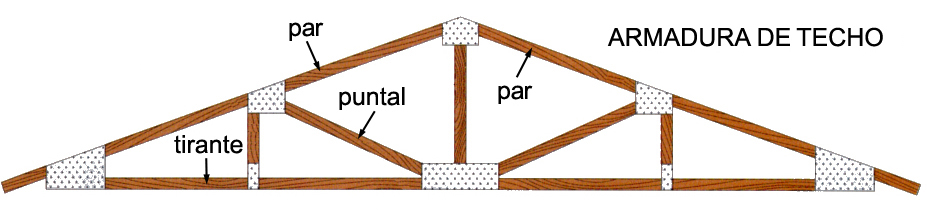
Por ser muy usada en el rubro de la construcción, la acepción más divulgada de estructura —tomada por muchos como su definición excluyente— es la correspondiente a estructuras portantes. Este tipo de estructura tiene la función de soportar pesos (cuyo prototipo es la armadura que sostiene un tejado, en Argentina frecuentemente denominada cabriada, véase la Figura 1) o de mantener unidas entre sí piezas (cuyo prototipo es el chasis de un automóvil o la carcaza de un aparato). Los siguientes son algunos tipos comunes de estructuras portantes:
|
Es un buen ejercicio discutir qué sostiene o mantiene unido cada uno, así como agregar ejemplos. No debe confundirse las estructuras portantes con contenedores como las mochilas, ollas, portafolios o vasijas de cualquier clase. La discusión de los rasgos comunes y diferenciales de ambas categorías ayuda mucho a fijar el concepto. Algunos de los rasgos a tener en cuenta para esta comparación son: si el artefacto es mayoritariamente cerrado o abierto, si las partes están sueltas o fijas; si la estructura es interior, exterior o ésto es indiferente; si los materiales a usar deben ser rígidos o flexibles.
La más sencilla y estable (en el sentido de difícil de deformar) de las estructuras portantes planas es la triangular, razón por la cual tanto la común armadura de techo como las complejas cúpulas geodésicas están hechos de estructuras triangulares. Si se analiza cuidadosamente la Figura 1 se descubrirá que la armadura está compuesta de una estructura principal triangular formada por 2 vigas de madera inclinadas (los dos pares que soportan directamente el tejado) y una horizontal (el tirante). Esta estructura está a su vez reforzada por 6 estructuras triangulares obtenidas mediante la fijación con piezas metálicas apropiadas (las punteadas de la figura) de 5 maderos más cortos. Esta estructura, si se hace de madera dura y sección suficientemente grande, es capaz de soportar, por ejemplo, el enorme peso de una cubierta de tejas.
Se cometería un gravísimo error didáctico si se creyera que la exhibición de la figura o la reiteración de las afirmaciones del párrafo anterior bastan para la asimilación de la estabilidad de las estructuras triangulares. Recién cuando el educando deba construir una estructura portante estable, como el bastidor de un telar, descubrirá el problema. El concepto es prototípico de los que requieren ser trabajados de manera concreta, sensorial y operativa: por experimentación y descubrimiento. Se propone para ello una secuencia de actividades que pueden y deben ser trabajadas en diferentes niveles educativos, actividades que —como es usual en Educación Tecnológica— requieren y trabajan simultáneamente saberes de otras áreas. En este caso, por tratarse de estructuras espaciales, los conocimientos básicos requeridos son los de la Geometría; al mismo tiempo, al mostrar su utilidad, pueden motivar el interés por su estudio. Un hecho central de la teoría del aprendizaje es que la adquisición de los saberes espontáneos, los que las personas son capaces de adquirir por sí mismas fuera de la escuela, está motivada por su valor práctico cotidiano.
Construcción de estructuras portantes simples con sorbetes e hilos de coser
Se puede construir facilmente y sin costo tanto estructuras planas como tridimensionales usando canutillos para sorber gaseosas (en Argentina llamados pajitas o sorbetes) e hilo común de coser. Para ello se pasan trozos de hilo suficientemente largos por el interior de sucesivas pajitas, anudándolos en vértices adecuados. Se ilustra el método con la construcción del tetraedro de la Figura 2. Se forma el primer triángulo pasando un hilo sucesivamente por el interior de los canutillos 1, 2 y 3 y anudando sus extremos. Se sujetan luego, de manera similar, los canutillos 4 y 5 al 3 del triángulo precedente, formando así dos triángulos articulados sobre el mismo eje (el lado 3). Se forma finalmente la base del tetraedro uniendo el canutillo 6 a los lados 2 y 5 (o 1 y 4) — pasando siempre el hilo a través de todos los canutillos involucrados. Es muy difícil pasar los hilos por el interior de las pajitas sin el auxilio de una herramienta apropiada. Es un valioso desafío plantear el diseño y construcción de la herramienta que permita hacerlo: un alambre fino (como los usados en las florerías) con un ojalillo en la punta. Esta parte de la actividad ilustra de modo concreto la necesidad y viabilidad de la fabricación de las propias herramientas de trabajo, destreza esencial para los artesanos.
Una vez que el docente haya hecho esta actividad preparatoria, puede proponer a los educandos la construcción con el mismo método de las siguientes dos estructuras planas simples: un triángulo y un cuadrado. Una vez hechas, se les pide que verifiquen la estabilidad de cada una de ellas. Los más pequeños seguramente se sorprenderán al descubrir la indeformabilidad del triángulo y la imposibilidad de mantener la forma cuadrada sin accesorios (por ejemplo, esquineros) que permitan la conservación de los ángulos rectos. Éste es un ejemplo de lo que Piaget denominaba conflictos cognitivos: la imposibilidad de comprensión de un hecho en base a los saberes preexistentes y la consiguiente promoción de la adquisición de nuevos saberes.
Para verificar la asimilación del concepto de estabilidad de las estructuras triangulares, es decir, la capacidad de los educandos de transferirlo a situaciones diferentes de las directamente experimentadas, se plantean los siguientes problemas:
- ¿Qué elemento agregarían a la estructura cuadrada para hacerla más estable? Construyan la nueva estructura verificando su propuesta (hipótesis).
- ¿Cuales creen que es el más estable de los poliedros regulares? ¿Por qué? Constrúyanlo, así como algún otro poliedro regular (el más simple después del tetraedro es el cubo) y compárenlos.
- ¿Se les ocurre un método general para hacer totalmente estable un polígono construido con canutillos e hilos?
La respuesta al primer problema es obviamente la formación de subestructuras triangulares mediante el agregado de una diagonal. Como la longitud de una diagonal es mayor que la de un lado y los canutillos típicamente tienen la misma longitud, se requiere disminuir por recorte los lados del cuadrado. Para calcular la disminución hay que usar el Teorema de Pitágoras, problema de nivel secundario avanzado o terciario. Los más pequeños pueden encontrarlo por prueba y error, recortando paulatinamente los canutillos que forman los lados (todos a la vez para asegurar su igualdad) hasta que la longitud del no recortado coincida con la diagonal del cuadrado. La técnica de formación de triángulos para estabilizar estructuras portantes es muy frecuente y puede verse en todo tipo de estructuras de acero, de las cuales la más famosa es la torre Eiffel. Son ejemplos comunes los puentes ferroviarios como el que se ilustra en la Figura 3 y el apuntalamiento de los postes esquineros de cualquier alambrado rural, pero basta mirar con cuidado a nuestro alrededor, en cualquier lugar que estemos, para encontrar uno equivalente. Los soportes de un estante (ménsulas) son un ejemplo, busque otros.
La respuesta al segundo problema es el tetraedro, único poliedro regular cuyas caras son todas triángulos. Es improbable que los niños más pequeños —que difícilmente hayan visto un tetraedro— encuentren por sí solos la respuesta. Será necesario entonces darles pistas como ¿Y si probamos enganchando triángulos? u otras similares. La realización más común de esta estructura es el trípode, que tiene además la virtud (consecuencia de la interesante propiedad geométrica tres puntos definen un plano) de que siempre queda bien asentado, por irregular que sea la superficie base. Las estructuras de este tipo también son sumamente comunes. Por ejemplo, los tensores que sostienen cualquier estructura delgada y muy alta (en Argentina denominados vientos), como una antena de radio, definen un tetraedro alargado (pirámide triangular). Nótese que tanto en el caso bi como en el tridimensional, la estabilidad no requiere que los triángulos formados sean equiláteros (revisite la Figura 1). La respuesta al tercer problema, que se esboza al final de este artículo, es la base de la construcción de cúpulas geodésicas como la de la Figura 5.
Explicación de la estabilidad de las estructuras portantes triangulares
Durante los más de 500.000 años de su evolución, a partir de las primeras herramientas de piedra, las tecnologías fueron descubiertas por azar y desarrolladas por ensayo y error. Es muy reciente la comprensión de que tan pronto se supera la etapa más rudimentaria estos métodos son ineficaces. Es necesario, por ello, crear en los educandos la conciencia de que las experiencias exclusivamente sensoriales y motrices, la experimentación, no es suficiente para el buen desarrollo de las tecnologías, se requiere también un análisis racional. Esto permitiría, si las hubiera, usar estructuras alternativas apropiadas al problema portante a resolver. Para ello se les plantea el siguiente problema:
- La dificultad de deformación de un triángulo,¿proviene de propiedades geométricas del triángulo, de las propiedades físicas de los materiales con que está hecho o de una combinación de ambas? Justifiquen su respuesta de la manera más racional posible.
Las estructuras triangulares hechas de materiales rígidos (como las pajitas) son capaces de mantener invariable su forma aunque las uniones en los vértices no sean rígidas, como se verificó experimentalmente en las actividades anteriores. Triángulos hechos de materiales flexibles, por ejemplo sólo de hilo, no tienen esta propiedad. Sin embargo, no basta la rigidez de los lados para hacer al polígono indeformable, como se vió con el cuadrado.
Cuando uno de sus lados (dos vértices) está sujeto y se aplica en el vértice restante una fuerza cualquiera, las estructuras triangulares tienen la propiedad (sólo demostrable en cursos avanzados de Mecánica) que los lados libres no experimentan torsiones, sólo compresiones o tracciones. Ningún otro polígono tiene esta propiedad, razón por la que su uso es tan generalizado en la industria de la construcción. Los demás polígonos, como los cuadrados, requieren esquineros para mantener invariable su forma (es decir, los ángulos en los vértices) y hay técnicas para su fácil construcción en el aula. Este tipo de explicación física no es viable en un nivel secundario o terciario, por lo que hay que hacer experiencias como la siguiente:
- Para que una estructura poligonal de lados rígidos pueda deformarse es necesario poder variar sus ángulos internos manteniendo constante la longitud de los lados. Entonces, ¿se pueden variar los ángulos internos de un triángulo sin variar la longitud de sus lados?
Se trata de un problema geométrico (científico) cuya respuesta negativa se justifica con la construcción de la Figura 4. Se parte del lado de longitud a comprendido entre los vértices P y Q. Sean b y c las longitudes de los dos lados restantes, el primero con vértice común con el primero en P y el segundo en Q. Se traza la circunferencia de centro P y radio b, primero, y luego la de centro Q y radio c. Estas circunferencias, indicadas con líneas de trazos en la figura adjunta, se intersectan a lo sumo en dos puntos, aquí denotados 1 y 2. Por lo tanto, hay a lo sumo dos triángulos, los PQ1 y PQ2 de la figura adjunta, cuyos lados tienen longitudes a, b y c. Ambos triángulos tienen los mismos ángulos internos y no hay posibilidad de pasar de uno a otro o de deformarlos sin variar la longitud de por lo menos uno de sus lados. En conclusión, la explicación de la estabilidad de los triángulos es una combinación de propiedades geométricas (imposibilidad de variar los ángulos internos sin variar la longitud de los lados) y físicas (debido a que la rigidez del material impide cambiar la longitud de los lados).
La cúpula geodésica
La culminación de las estructuras portantes basadas en triángulos es la esfera o cúpula geodésica inventada por el arquitecto estadounidense Buckminster Fuller (1895-1983). Está basada en la estructura del icosaedro truncado inventado por el geómetra griego Arquímedes (287-212 aC), la forma de la pelota olímpica de fútbol (véase Ghyka). Las caras de este poliedro son exágonos y pentágonos cuyos ángulos interiores se estabilizan mediante pirámides triangulares. El resultado es una estructura extremadamente liviana y resistente, como la del Epcot Center que se muestra en la Figura 5. Se ha marcado allí, para mejor comprensión de la estructura, un pentágono y un exágono, ya que las pirámides triangulares son claramente visibles.
Reflexiones didácticas finales
Además de ilustrar el desarrollo espiralado del concepto de estructura (reintroducción en diferentes niveles escolares sucesivos), las actividades muestran claramente la combinación de procedimientos (experimentación, técnica de construcción usando canutillos e hilos), saberes (razonamientos sobre propiedades geométricas de triángulos y tetraedros) y de actitudes (motivación por la necesidad de resolver conflictos cognitivos). El principal aspecto didáctico es que todos los contenidos y actividades están centrados, como debe ser siempre en la Educación Tecnológica, en la resolución de un problema práctico: la construcción de estructuras portantes efectivas y su reconocimiento en contextos familiares, preferentemente no escolares. Se recalca y se proponen modos de evaluar la asimilación del concepto mediante su aplicación a situaciones diferentes de las ejemplificadas en clase, verificación imprescindible para no cometer el error de fomentar un conocimiento meramente memorístico. Finalmente, nótese que se evita cuidadosamente el error de comenzar las actividades con una definición de estructura portante, solamente se dan sus rasgos esenciales. El desarrollo espiralado requiere que la definición no sea el punto de partida sino parte del resultado final del proceso de elaboración personal del concepto.
Fuentes
- Solivérez, Carlos E.; Introducción a las estructuras; revista Novedades Educativas N° 163; Buenos Aires; julio de 2004; pp. 12‑15.
- Ghyka, Matila C.; Estética de las proporciones en la naturaleza y en las artes; Editorial Poseidón; Buenos Aires; 1953; pp. 87‑95.
- Descarga de la versión original de este artículo en formato pdf:
 Estructuras portantes por Carlos E. Solivérez.
Estructuras portantes por Carlos E. Solivérez.