Cómo armar poliedros

Figura 1. Pantalla de lámpara con estructura de
rombicuboctaedro hecha con esquineros.

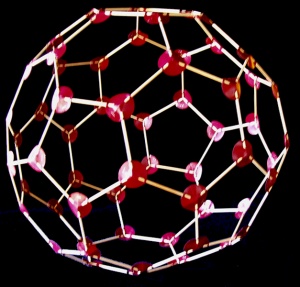
La construcción de poliedros desarmables hechos de varillas y esquineros es una técnica que tiene al menos 2 funciones importantes. La primera es facilitar la asimilación del importante concepto abstracto de estructura mediante su realización concreta en el caso geométrico de los poliedros, donde los elementos son las aristas (varillas) y las relaciones son los ángulos entre aristas (determinados por los ojales de los esquineros que las sujetan) y las distancias entre vértices (dados por la longitud de las varillas). La segunda aplicación es permitir al docente disponer de conjuntos de cuerpos fácilmente transportables sin el riesgo de rotura de los hechos de otros modos. Se explican aquí todos los pasos a seguir para la construcción de cualquier poliedro —regular o no, convexo o no— y se dan sugerencias sobre materiales que pueden usarse en la tarea, incluyendo algunos reciclados. Se dan los esquineros que permiten la construcción de los 5 sólidos platónicos (tetraedro, cubo, octaedro, icosaedro y dodecaedro) y de algunos de los bellos poliedros arquimedianos, como el ilustrado en la Figura 1. En estas categorías de poliedros, para los cuales los esquineros son todos similares y las varillas tienen todas la misma longitud, se obtiene al mismo tiempo una prueba constructiva de que están unívocamente determinados por los ángulos poliedros y la longitud de arista, concepto geométrico de gran valor práctico.

Materiales, útiles, técnicas e información requeridas

• Materiales
  • esquineros: envases TetraPak® reciclados o tapas de fotocopias anilladas en desuso o cartulina gruesa preferentemente plastificada.
  • aristas: varillas para brochettes de buena calidad o varillas de madera torneada.
  • adhesivo en barra.
• Útiles
  • calibre;
  • tijera;
  • trincheta ("cúter");
  • sacabocados del diámetro (holgado) de las varillas a usar;
  • abrochadora.
• Información
  • patrones de los esquineros requeridos para el poliedro a construir.
• Técnicas
  • corte con trincheta ("cúter");
  • troquelado con sacabocado;
  • abrochado con abrochadora;
  • medición de diámetros de varillas con calibre;
  • medición de ángulos con transportador (sólo para hacer patrones no provistos aquí).

Método de construcción y recomendaciones

Figura 2. Icosaedro truncado
hecho con el método aquí descripto.

El método de construcción es la unión de varillas de madera (las aristas del poliedro) con esquineros que las sujetan para formar el ángulo poliedro en cada vértice. Conviene usar palitos de brochette como varillas, que tienen usualmente unos 4 mm de diámetro y 24 cm de longitud y son de bajo costo y gran dureza. Sin embargo, no cualquier tipo es apropiado y debe verificarse que su superficie sea lisa y que sus diámetros sean uniformes. Pueden usarse varillas de madera torneada, pero son mucho más caras y usualmente menos resistentes. Los palitos deben recortarse del largo apropiado al tamaño final del cuerpo que se quiere construir, el valor del diámetro de la esfera D que circunscribe los sólidos regulares y semirregulares. Pueden usarse enteros para los poliedros regulares y partidos por la mitad para los arquimedianos, donde podrían obtenerse cuerpos demasiado grandes y pesados.

Los esquineros delimitan los ángulos poliedros en cada vértice, por lo que deben ser capaces de conservar bien su forma (tener suficiente rigidez) y sostener sin desgarrarse las varillas que atraviesan sus ojales. El material más barato que cumple estas condiciones es el laminado usado en los envases TetraPak&reg. Es más resistente y de mejor presentación el material de con que se hacen las tapas de documentos fotocopiados y anillados. Las tapas de cuadernos, otro material reciclable, suelen ser demasiado gruesas, poco flexibles y fácilmente desgarrables, aunque ésto no es regla general.

En los poliedros convexos regulares y arquimedianos (ver Tabla 1) las aristas determinan ángulos poliedros por confluencia de 3 a 5 caras en cada vértice. La razón de esta limitación es que en estos poliedros el menor ángulo interno de una cara es 60° (triángulo equilátero), el número mínimo de caras en un vértice es 3 (de lo contrario se delimita un plano, no un volumen) y pueden haber a lo sumo 5 triángulos equiláteros concurrentes en el mismo vértice para que el ángulo poliedro no sea plano (las suma de los ángulos internos de las caras en el vértice común debe ser menor de 360°).

Figura 3. Patrón genérico de esquinero para un triedro.

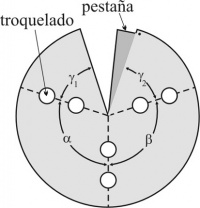
En cada vértice los ángulos entre aristas son los ángulos internos de las caras (polígonos regulares) que confluyen allí. El patrón general de un esquinero con tres aristas (triedro) es el de la Figura 3. La zona más oscura es la pestaña que permite fijar el borde opuesto por superposición y abrochado. Los cortes deben efectuarse por las líneas continuas con tijera (los bordes) y sacabocados (los círculos). Se facilita el abrochado de la pestaña si se dobla levemente la esquina contigua a la pestaña señalada con un punto en la Figura 3. Éste sirve de tope para sujetar el borde cuando se lo abrocha con la otra mano de modo que tape exactamente la pestaña. Si el material ha sido bien elegido no es necesario reforzar esta unión usando cemento de contacto o cola vinílica.

Los dobleces, marcados con líneas de trazos, corresponden a la posición de las varillas. Los ángulos α, β y

γ = γ₁ + γ₂

son los internos de los 3 polígonos que tienen por vértice común el centro del esquinero (3, 4 o 5 en el caso general). Lo más efectivo y simple es tomar

γ₁ = γ₂= γ/2.

En base a las consideraciones anteriores es fácil diseñar un esquinero para cualquier vértice, trátese o no de un poliedro convexo o regular, teniendo en cuenta que deben haber tantos dobleces como aristas convergen en el vértice. Por ejemplo, el esquinero correspondiente a un cubo (exaedro) tiene los siguientes ángulos:

α = β = γ = 90°, γ₁ = γ₂ = 45°

y hay tantos dobleces como aristas: 3. Aunque los ejemplos dados más abajo corresponden a poliedros regulares o arquimedianos, mutatis mutandi (con las modificaciones que correspondan) el método permite construir los esquineros para cualquier poliedro. La Figura 4 muestra los patrones correspondientes a todos los sólidos platónicos y algunos de los poliedros arquimedianos. Allí se denomina, por simplicidad, "farol" al rombicuboctaedro y "pelota" al icosaedro truncado.

Archivo:Poliedros esquineros selectos.jpg

Esquineros de los sólidos platónicos y algunos arquimedianos.

Figura 5. Varilla insertada en esquinero.

Un problema frecuente con los palitos de brochette —especialmente con los más baratos— es que en un mismo paquete suelen tener varios diámetros diferentes. Seleccione y use sólo los de un mismo diámetro, que debe usar para hacer las plantillas o patrones que servirán de guía para el corte de los esquineros. Como guía para todos los cortes y dobleces se usan fotocopias del patrón pegadas con unos pocos toques de adhesivo sólido (no use otro, pues se busca poca adherencia) sobre la cara menos linda de la lámina. Una vez finalizados los cortes y hechos los dobleces (que conviene planchar con algún objeto suave, como el cuerpo de una lapicera), el papel puede sacarse facilmente de la superficie plastificada, humedeciendo el papel cuando sea necesario. Para obtener con facilidad los patrones necesarios, haga una fotocopia con tantos ejemplares del patrón como esquineros se quieren cortar. Al final de esta guía encontrará algunos ejemplos.

el que debe usar para cortar los ojales indicados con círculos la Figura 3.Las aberturas circulares se troquelan de diámetro levemente superior al de las varillas, lo que puede hacerse con poco esfuerzo con un sacabocados. Las varillas se hacen pasar a través de ellas como se muestra en la Figura 4. El material del esquinero no debe ser demasiado grueso para poder formar en su interior la presilla que sujeta a la varilla. Esto se ilustra en esta figura, donde la fotografía de la izquierda muestra la parte interior del esquinero (cara cóncava) y la derecha la exterior (cara convexa). De este modo el doblez hecho por la línea de trazos soporta la mayor parte de la varilla, mientras que la mayor deformación se localiza en la pequeña parte de la presilla, donde el riesgo de rotura es máximo.

Las estructuras construidas de esta manera, aunque sólo soportan su propio peso, permiten obtener formas muy variadas con mínimo gasto en materiales. Se requiere, eso sí, paciencia y prolijidad para fabricar bien los esquineros apropiados para cada vértice, cortar las varillas a la longitud apropiada y aguzarlas para facilitar su colocación.

Poliedros regulares y semirregulares

Las caras de los deltaedros, poliedros convexos, son todos polígonos regulares idénticos (triángulos equiláteros) pero no cumplen la condición de congruencia de los ángulos poliedros que determinan las aristas que confluyen en todos y cada uno de los vértices.

La Figura 5 es la fotografía de un icosaedro truncado (estructura de la pelota de fútbol olímpica) armada con varillas de brochettes de 12 cm de largo, lo que le da un diámetro final aproximado de 55 cm.

Impresión de patrones

Es fácil recortar los esquineros cuando se usa un patron de guía para cada uno. Para eso se necesita fotocopiar tantos patrones como esquineros hay, es decir, como vértices tiene la estructura (ver la Tabla 2 para los poliedros regulares y algunos semirregulares). El número de fotocopias a hacer se disminuye drásticamente si se usa la siguiente técnica:

• Se hace primero el patrón y luego se lo fotocopia (van 1 fotocopias y 2 ejemplares).
• Recortando el patrón, se fotocopia el conjunto de dos patrones así armado (van 2 fotocopias y 4 ejemplares).
• Se fotocopian luego los 4 ejemplares que ya se tienen, para obtener 8 (van 3 fotocopias y 8 ejemplares).
• En cada etapa, al fotocopiar conjuntamente los patrones originales con sus fotocopias, se duplica el número de ejemplares. Esta duplicación es válida hasta el límite del tamaño de la hoja, que si es de formato legal (21,5 ·35,6 cm) puede contener unos 21 patrones. De allí en más se fotocopian hojas completas.

Como se ve, la técnica es muy eficiente. Para hacer los patrones de los 90 esquineros que conforman la pelota de fútbol, se requieren solamente 7 fotocopias y sobran algunos de reemplazo (haga la cuenta, sumando todos los ejemplares sucesivamente obtenidos). Si se tiene una PC, un digitalizador y un programa de dibujo, se puede armar la hoja completa de patrones de una sola vez, lo cual reduce el número de fotocopias a hacer.

Etapas del armado de una estructura

El siguiente es un resumen de las principales etapas del armado:

• Comienza armando una estructura de patrón conocido, antes de intentar diseñar patrones nuevos.
• Cuenta la cantidad de vértices de cada tipo y diseña el patrón correspondiente a cada uno.
• Para diseñar el patrón debes conocer primero los ángulos internos de las caras que tienen ese vértice en común. Si la cara es un polígono regular de n lados, sus ángulos internos son todos iguales y valen α = (n – 2)·180°/n.
• El esquinero del vértice debe tener tantos dobleces como caras confluyen en él.
• Haz solo 1 patrón de cada tipo. Luego multiplícalos por fotocopiado o digitalización computada hasta tener la cantidad total necesaria y algunos más, para reponer cualquier rotura.
• Recorta los patrones unos milímetros por fuera de su borde. El corte por las líneas se hará cuando esté pegado.
• Pega los patrones con unos pocos toques de adhesivo sólido sobre el lado no aluminizado de la lámina de TetraPak®, evitando hacerlo sobre un pliegue del envas. Recorta luego cuidadosamente con tijera por las líneas continuas exteriores. Respeta el receso de la pestaña.
• Determina la longitud de varilla apropiada para la estructura. Selecciona la cantidad necesaria usando el calibre para verificar que todas tienen el mismo diámetro.
• Usa un sacabocados del mismo diámetro o levemente superior al de la varilla. Con un diámetro inferior, tendrás dificultades en la introducción de las varillas con riesgo de rotura del esquinero. Si el agujero es demasiado gran de, la varilla quedará suelta y la estructura se desarmará. Prueba con un esquinero armado, si cuesta mucho introducir la varilla, aumenta el diámetro de los agujeros a la medida siguiente, verificando que no se suelte.
• Pliega los esquineros por las líneas de trazos, asentando bien el doblez con un objeto redondeado y suave.
• No comiences el abrochado de los esquineros hasta que todos estén recortados, plegados: la pericia que brinda el trabajo repetitivo disminuye los errores y el tiempo de realización de las tareas. Retira el papel patrón antes de comenzar a abrochar.
• Se cortan las varillas de la misma longitud, es decir se la igualan a la varilla de menor longitud, afilando levemente las puntas con un sacapuntas o una trincheta para facilitar su introducción.

Fuentes

La técnica aquí descripta fue desarrollada por Carlos E. Solivérez para los cursos de Tecnología del Instituto de Formación Docente de San Carlos de Bariloche, entre los años 2000 y 2004.

{{Subst:Menor que}}Gallery caption="Esquineros selectos" widths=200 heights=200 perrow=4>
Archivo:Esquinero tetraedro.jpg|<center>Tetraedro</center>
Archivo:Esquinero cubo.jpg|<center>Cubo</center>
Archivo:Esquinero octaedro.jpg|<center>Octaedro</center>
Archivo:{{{8}}}|<center>{{{9}}}</center>
</Gallery>