Rompecabezas geométricos

Los rompecabezas geométricos son figuras geométricas, bi o tridimensionales, que deben componerse o descomponerse de manera prefijada. Aunque usualmente planteados como un juego de paciencia más que de ingenio, los que aquí se presentan tienen el interés científico de favorecer el desarrollo de conceptos geométricos importantes.

Partición triángulo equilátero — cuadrado

Las dos figuras geométricas regulares planas más simples son el triángulo equilátero y el cuadrado. Si se elige un segmento de una longitud cualquiera, hay un único triángulo plano cuyos tres lados tienen la misma longitud que ese segmento, el equilátero. No sucede lo mismo con el cuadrado (o las restantes figuras regulares planas) ya que hay infinitos cuadriláteros (rombos) que tienen 4 lados de idéntica longitud. Para construir el cuadrado es necesario agregar las condiciones adicionales de que los ángulos internos sean todos iguales, lo que equivale a pedir que valgan 90° (la demostración de la equivalencia de ambas condiciones es un interesante problema geométrico). Un problema de carácter muy general que ha suscitado muchos desarrollos matemáticos es la construcción con regla, transportador y compás (la mayoría de los geómetras profesionales prefieren prescindir del transportador) de 2 figuras regulares diferentes con la misma área (caso de la denominada cuadratura del círculo) o con áreas con una relación de proporcionalidad determinada (caso de la determinación del número pi o π). En el caso que se discute aquí deben construirse, aunque de una manera muy particular, un triángulo equilátero y un cuadrado que tienen la misma área. Según un teorema demostrado por uno de los más importantes matemáticos del siglo XIX, el alemán David Hilbert, cualquier polígono (regular o no) puede transformarse en cualquier otro mediante su partición en un número finito de partes. En el caso de un triángulo equilátero el número mínimo de partes cuyo reordenamiento conduce a un cuadrado es 4, como surge de la necesidad de generar sus 4 ángulos rectos. El rompecabezas que aquí se presenta es una de las maneras de generar tal subdivisión del triángulo equilátero (¿cuántas más hay?), propuesta por un experto en matemática recreativa, el inglés Henry Ernest Dudeney en su primer libro, The Canterbury Puzzles.

Animación de la transición de triángulo equilátero a cuadrado.

Partición del triángulo equilátero

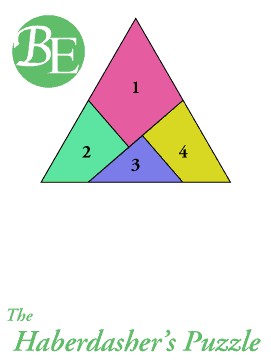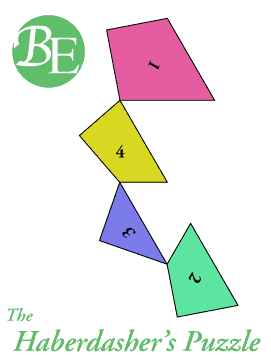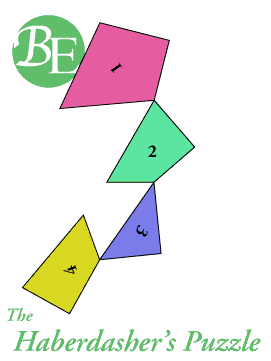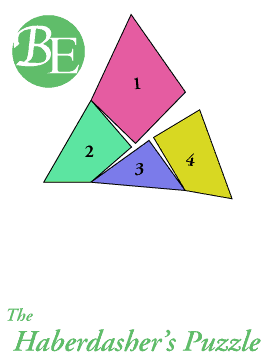
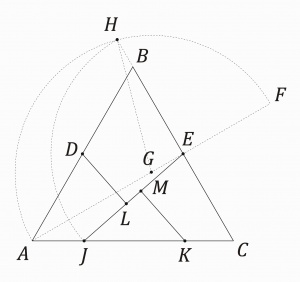
La partición de Dudeney del triángulo equilátero ABC, ilustrada en la figura de la izquierda, tiene las siguientes etapas: Se determina el centro D del lado AB. Se hace lo mismo con el lado BC determinando el punto E. Se traza el segmento AF, con origen en A, tal que EF = BE. Se determina el punto medio G del segmento AF. Con centro en G, se traza el arco de circunferencia superior con extremos en A y F. Se prolonga el lado CB hasta intersectar el arco anterior en H. Con centro en E, se traza el arco de circunferencia que pasa por H e intersecta al lado CA en J. Se determina, sobre CA, el punto K tal que JK = BE. Se traza, por el punto D, la perpendicular a JE que determina el punto L. Se traza, por el punto K, la perpendicular a JE que determina el punto M. Nótese la formación de los ángulos rectos con vértices en L y M. Tanto la partición de los lados en mitades como el trazado de las perpendiculares se debe hacer con compás de mina bien afilada o pluma fina, procedimiento más preciso que la medición de longitudes. Los segmento indicados con trazo continuo determinan la división del triángulo equilátero en 4 partes que permiten formar un cuadrado. El triángulo JKM y el cuadrilátero BELD parecen ser simétricos pero no lo son. La exactitud matemática de la construcción, que se ignora cómo fue concebida por Dudeney, fue rigurosamente demostrada por el matemático Chester Hawley.

Partición del triángulo equilátero para armar un cuadrado.

Construcción del rompecabezas

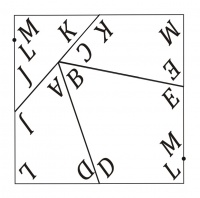
En la figura de la derecha se muestra la distribución de las piezas del triángulo equilátero para formar el cuadrado. Esta distribución es la más apropiada para construir el rompecabezas con el (usualmente) mínimo desperdicio de material. La identificación de los puntos facilita ubicar la posición de las piezas en la figura previa. La fabricación del rompecabezas puede hacerse con láminas de guillermina (un aglomerado de aserrín), material barato y fácil de trabajar con un serrucho de costilla (véase el artículo útiles básicos). Esta herramienta permite hacer cortes rectos con más facilidad que la sierra de calar usualmente recomendada para tareas de esta clase. Es importante hacer una plantilla que sirva de guía a los cortes, una fotocopia a escala apropiada de la figura adjunta. Debe tenerse especial cuidado en hacer los cortes por el centro de las líneas, ya que pequeños apartamientos amplifican las fallas de encaje en la figura del triángulo equilátero. Luego hay que proteger este material blanco con barniz brillante (previo teñido con el color deseado) o esmalte sintético. Si se quiere hacer un uso exclusivamente recreativo del rompecabezas se pueden fabricar las piezas con materiales más atractivos, como metales, maderas nobles y vidrios con tratamientos superficiales adecuados. Como se ilustra en la animación de la parte superior, si se encadenan las piezas de modo apropiado puede pasarse del triángulo equilátero al cuadrado (y viceversa) mediante una simple rotación de las mismas sobre una superficie plana.

Partición del cuadrado para armar un triángulo equilátero.

Uso didáctico del rompecabezas

Rompecabezas construido.

Pistas para el reordenamiento de piezas.

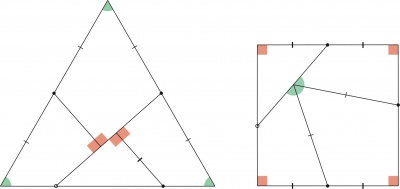
Para un uso didáctico hay que hacer énfasis, como claves del armado, en propiedades geométricas de importancia. En este caso conviene pintar ambos lados de todas las piezas del mismo color para no dar otras claves que los ángulos internos y la igualdad de los bordes coincidentes. Los ángulos de interés son los rectos (90°) del cuadrado, identificados con cuadrados naranja en la figura Pistas para el reordenamiento de piezas. Estos ángulos deberían ser fácilmente identificables y no requerir marcado, pero no suce lo mismo con los de 60° del triángulo equilátero, identificados con sectores circulares verdes en la misma figura. Estos ángulos son difíciles de diferenciar de otros ángulos agudos parecidos pero no iguales, por lo que requieren alguna marca identificatoria. La igualdad de los lados es una pista más difícil de interpretar, sólo aplicable en la construcción del cuadrado y para las piezas cuadrangulares. Los lados iguales se han identificado en la mencionada figura con cortos segmentos transversales en el punto medio de los lados, delgados para el caso de los segmentos de longitud igual a la mitad del lado de triángulo equilátero y gruesos para los que tienen la mitad de la longitud del lado del cuadrado.

¿Es posible esta descomposición?

Se propone el siguiente proceso de aprendizaje del armado, en orden creciente de dificultad:

1. Nivel elemental (3 a 5 años)
   • "Encadenar" los piezas con hilo de coser delgado (preferentemente de algodón), a través de pequeñas perforaciones hechas en los extremos de las piezas marcadas con pequeños circulos negros. El uso de hilo delgado de algodón minimiza la probabilidad de la rotura de las puntas en caso de que se retuerzan las piezas. Superada esta etapa hay que cortar los hilos, dejando las piezas sueltas.
2. Nivel medio (6 a 12 años)
   1. Señalar la igualdad de los ángulos en los vértices externos tanto del triángulo equilátero (60°) como del cuadrado (90°). Ejercicios previos de reconocimiento de ambos tipos.
   2. Señalar la importancia de la buena coincidencia de las longitudes de las piezas adosadas y el carácter rectilíneo de los bordes exteriores.
3. Nivel avanzado (mayores de 12 años)
   • Dar vuelta (invertir) al azar las piezas para aumentar el grado de dificultad del armado, ya que ninguna de ellas es simétrica con su invertida.
4. Nivel técnico (saberes avanzados de Trigonometría)
   • Análisis de la posibilidad de descomponer el triángulo equilátero de la manera indicada en la figura ¿Es posible esta descomposición?. Además de una verificación directa por corte del dibujo en papel, el análisis debe incluir los cálculos del valor del lado del cuadrado en función del del triángulo equilátero y de tantos otros lados o ángulos como sean necesarios para asegurar la posibilidad o imposibilidad de la partición propuesta.

Fuentes

• Dudeney, Henry Ernest; The Canterbury Puzzles; versión htlm del Proyecto Gutenberg. El rompecabezas se describe en la sección 26 con el nombre The Haberdasher's Puzzle (El Problema del Mercero), pues es planteado para un corte de tela.
• Gardner, Martin; More Mathematical Puzzles and Diversions; Penguin Books; 1977 (6ª reimpresión); pp. 25‑27.
• Hawley, Chester W.; A Further Note on Dissecting a Square into an Equilateral Triangle; revista The Mathematics Teacher; February 1960.

Fuentes generales

• Scientific American: sección de juegos matemáticos de esta revista estadounidense de divulgación científica.
• Hiele, Pierre van; Desarrollando el pensamiento geométrico a través de actividades que comienzan como un juego; revista Teaching Children Mathematics, vol. 5, Nº6; February 1999; pp. 310‑316.
• Kasner, Edward & Newman, James R.; Matemáticas e imaginación; Hyspamérica Ediciones; Madrid (España); 1985; ISBN 9788485471553 (Kasner&Newman MI).