Diferencia entre revisiones de «Poliedros arquimedeanos»
La enciclopedia de ciencias y tecnologías en Argentina
m |
m (Poliedros arquimedianos trasladada a Poliedros arquimedeanos) |
||
| (No se muestran 7 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
| − | + | Los '''poliedros arquimedeanos''' o '''sólidos arquimedeanos''' son [http://es.wikipedia.org/wiki/Poliedro_convexo poliedros convexos] cuyas caras son [http://es.wikipedia.org/wiki/Pol%C3%ADgono_regular polígonos regulares] de 2 o 3 clases diferentes, cuyas [http://es.wikipedia.org/wiki/Arista_(geometr%C3%ADa) aristas] son todas de igual longitud y todos sus [http://es.wikipedia.org/wiki/Vértice_(geometr%C3%ADa) vértices] son puntos de la esfera que los circunscribe. Los ángulos poliedros que determinan las aristas en cada vértice son todos [http://es.wikipedia.org/wiki/Congruencia_(geometr%C3%ADa) congruentes]. Aunque tienen variadas aplicaciones, estos cuerpos son de interés más por su bella e intrigante forma y sus ricas propiedades geométricas que por su utilidad práctica. | |
| − | Los '''poliedros | ||
==Rasgos principales== | ==Rasgos principales== | ||
| − | Un poliedro o sólido | + | Un poliedro o sólido arquimedeano tiene los siguientes rasgos: |
# El segmento determinado por 2 vértices cualesquiera es siempre interior al cuerpo (es un poliedro convexo). | # El segmento determinado por 2 vértices cualesquiera es siempre interior al cuerpo (es un poliedro convexo). | ||
| Línea 11: | Línea 10: | ||
# Todas sus aristas tienen la misma longitud. | # Todas sus aristas tienen la misma longitud. | ||
# Los [http://es.wikipedia.org/wiki/Ángulo_poliedro ángulos poliedros] determinados por las aristas que convergen en cada vértice son convexos (es un polígono convexo). Es decir, la suma de los ángulos internos de todas las caras con un vértice común es menor que 360°. Esto limita drásticamente las combinaciones de polígonos regulares que pueden formar las caras. | # Los [http://es.wikipedia.org/wiki/Ángulo_poliedro ángulos poliedros] determinados por las aristas que convergen en cada vértice son convexos (es un polígono convexo). Es decir, la suma de los ángulos internos de todas las caras con un vértice común es menor que 360°. Esto limita drásticamente las combinaciones de polígonos regulares que pueden formar las caras. | ||
| − | # Sus caras pertenecen a 2 o a lo sumo a 3 de las siguientes categorías de polígonos regulares: [http://es.wikipedia.org/wiki/Triángulo_equilátero triángulos equiláteros],[http://es.wikipedia.org/wiki/Cuadrado cuadrados], [http://es.wikipedia.org/wiki/Pentágono pentágonos], [http://es.wikipedia.org/wiki/Hexágono exágonos], [http://es.wikipedia.org/wiki/Octágono octógonos] y [http://es.wikipedia.org/wiki/Decágono decágonos]. | + | # Sus caras pertenecen a 2 o a lo sumo a 3 de las siguientes categorías de polígonos regulares: [http://es.wikipedia.org/wiki/Triángulo_equilátero triángulos equiláteros], [http://es.wikipedia.org/wiki/Cuadrado cuadrados], [http://es.wikipedia.org/wiki/Pentágono pentágonos], [http://es.wikipedia.org/wiki/Hexágono exágonos], [http://es.wikipedia.org/wiki/Octágono octógonos] y [http://es.wikipedia.org/wiki/Decágono decágonos]. |
# Los [http://es.wikipedia.org/wiki/Ángulo_poliedro ángulos poliedros] determinados por las aristas que convergen en cada vértice son congruentes, es decir, pueden superponerse exactamente por traslaciones, rotaciones o/y reflexiones. Ésto permite construirlos de modo simple usando "esquineros" similares para todos los vértices. | # Los [http://es.wikipedia.org/wiki/Ángulo_poliedro ángulos poliedros] determinados por las aristas que convergen en cada vértice son congruentes, es decir, pueden superponerse exactamente por traslaciones, rotaciones o/y reflexiones. Ésto permite construirlos de modo simple usando "esquineros" similares para todos los vértices. | ||
| − | # Satisface (por ser un poliedro convexo) la relación de Euler[http://www.ics.uci.edu/~eppstein/junkyard/euler/] Nº de vértices + Nº de caras – Nº de aristas = 2, como puede verificarse directamente de la tabla inferior. | + | # Satisface (por ser un poliedro convexo) la relación de Euler[http://www.ics.uci.edu/~eppstein/junkyard/euler/]: Nº de vértices + Nº de caras – Nº de aristas = 2, como puede verificarse directamente de la tabla inferior. |
| − | El uso combinado de las relaciones 5 y 8 permiten determinar la cantidad de sólidos | + | El uso combinado de las relaciones 5 y 8 permiten determinar la cantidad de sólidos arquimedeanos posibles. Usualmente se considera que hay 15 poliedros arquimedeanos diferentes, donde 2 de ellos son enantiomorfos (imágenes especulares) de otros 2. El número que satisface la definición inicial es en realidad infinito porque incluye todos los [http://es.wikipedia.org/wiki/Prisma_(geometr%C3%ADa) prismas] y [http://es.wikipedia.org/wiki/Antiprisma antiprismas] de caras laterales son cuadrados o triángulos equiláteras y cuyas bases son cualquiera de los infinitos polígonos regulares, exceptuando al cuadrado (este prisma coincide con el cubo). Por esta razón es usual, aunque no hay consenso universal al respecto, excluir a los prismas y antiprismas de la lista de poliedros arquimedeanos. |
| − | La tabla siguiente da algunos datos importantes de los poliedros | + | La tabla siguiente da algunos datos importantes de los poliedros arquimedeanos. En ''tipos de caras'' se especifica la cantidad de caras que pertenece a cada tipo de polígono regulare. Los ''ángulos en vértices'' son los determinados por las aristas que convergen en un vértice y se dan en sentido horario mirando desde el interior del poliedro. ''D'' es el diámetro de la esfera en la está circunscripto el poliedro y se expresa en términos de la longitud ''a'' de las aristas[http://mathworld.wolfram.com/ArchimedeanSolid.html]. Los dos últimos datos son indispensables para el método constructivo que se da en el artículo [[Cómo armar poliedros]]. El grupo puntual, que no se discutirá aquí, identifica matemáticamente las [[simetrías]] de cada poliedro. |
<br> | <br> | ||
| Línea 70: | Línea 69: | ||
* [http://en.wikipedia.org/wiki/Archimedean_solid Archimedean solid] en Wikipedia en inglés. | * [http://en.wikipedia.org/wiki/Archimedean_solid Archimedean solid] en Wikipedia en inglés. | ||
* Uzquiano, Gabriel; ''¿Qué es un poliedro?''; revista Investigación y Ciencia; septiembre 2011; pp. 91‑93. | * Uzquiano, Gabriel; ''¿Qué es un poliedro?''; revista Investigación y Ciencia; septiembre 2011; pp. 91‑93. | ||
| + | |||
| + | ==Véase también== | ||
| + | * [[Cómo armar poliedros]]. | ||
<br> | <br> | ||
| Línea 75: | Línea 77: | ||
[[Categoría:Matemática]] | [[Categoría:Matemática]] | ||
| + | [[Categoría:glosario]] | ||
Revisión actual del 11:14 31 mar 2014
Los poliedros arquimedeanos o sólidos arquimedeanos son poliedros convexos cuyas caras son polígonos regulares de 2 o 3 clases diferentes, cuyas aristas son todas de igual longitud y todos sus vértices son puntos de la esfera que los circunscribe. Los ángulos poliedros que determinan las aristas en cada vértice son todos congruentes. Aunque tienen variadas aplicaciones, estos cuerpos son de interés más por su bella e intrigante forma y sus ricas propiedades geométricas que por su utilidad práctica.
Rasgos principales
Un poliedro o sólido arquimedeano tiene los siguientes rasgos:
- El segmento determinado por 2 vértices cualesquiera es siempre interior al cuerpo (es un poliedro convexo).
- Todos sus vértices son puntos de una esfera de diámetro D (esfera circunscripta, véase la tabla inferior).
- Sus caras son polígonos regulares de por lo menos 2 tipos diferentes (es semirregular).
- Todas sus aristas tienen la misma longitud.
- Los ángulos poliedros determinados por las aristas que convergen en cada vértice son convexos (es un polígono convexo). Es decir, la suma de los ángulos internos de todas las caras con un vértice común es menor que 360°. Esto limita drásticamente las combinaciones de polígonos regulares que pueden formar las caras.
- Sus caras pertenecen a 2 o a lo sumo a 3 de las siguientes categorías de polígonos regulares: triángulos equiláteros, cuadrados, pentágonos, exágonos, octógonos y decágonos.
- Los ángulos poliedros determinados por las aristas que convergen en cada vértice son congruentes, es decir, pueden superponerse exactamente por traslaciones, rotaciones o/y reflexiones. Ésto permite construirlos de modo simple usando "esquineros" similares para todos los vértices.
- Satisface (por ser un poliedro convexo) la relación de Euler[1]: Nº de vértices + Nº de caras – Nº de aristas = 2, como puede verificarse directamente de la tabla inferior.
El uso combinado de las relaciones 5 y 8 permiten determinar la cantidad de sólidos arquimedeanos posibles. Usualmente se considera que hay 15 poliedros arquimedeanos diferentes, donde 2 de ellos son enantiomorfos (imágenes especulares) de otros 2. El número que satisface la definición inicial es en realidad infinito porque incluye todos los prismas y antiprismas de caras laterales son cuadrados o triángulos equiláteras y cuyas bases son cualquiera de los infinitos polígonos regulares, exceptuando al cuadrado (este prisma coincide con el cubo). Por esta razón es usual, aunque no hay consenso universal al respecto, excluir a los prismas y antiprismas de la lista de poliedros arquimedeanos.
La tabla siguiente da algunos datos importantes de los poliedros arquimedeanos. En tipos de caras se especifica la cantidad de caras que pertenece a cada tipo de polígono regulare. Los ángulos en vértices son los determinados por las aristas que convergen en un vértice y se dan en sentido horario mirando desde el interior del poliedro. D es el diámetro de la esfera en la está circunscripto el poliedro y se expresa en términos de la longitud a de las aristas[2]. Los dos últimos datos son indispensables para el método constructivo que se da en el artículo Cómo armar poliedros. El grupo puntual, que no se discutirá aquí, identifica matemáticamente las simetrías de cada poliedro.
| Nombre | Imagen | Vértices | Ángulos en vértices |
Aristas | D[3] | Caras | Tipos de caras |
Grupo puntual |
Fuentes |
|---|---|---|---|---|---|---|---|---|---|
| Tetraedro truncado | 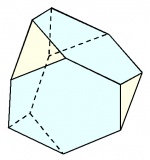 |
12 | 60° - 120° - 120° | 18 | √(11/2)a ≅ 2,3a | 8 | 4 exágonos 4 triángulos |
Td | [4] |
| Cuboctaedro | 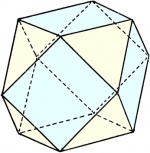 |
12 | 60° - 90° - 60° - 90° | 24 | 2a | 14 | 6 cuadrados 8 triángulos |
Oh | [5] |
| Cubo truncado | 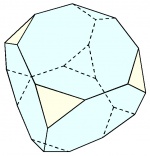 |
24 | 60° - 135° - 135° | 36 | 14 | 6 octógonos 8 triángulos |
Oh | [6] | |
| Octaedro truncado o tetrakaidecaedro o eptaparaleloedro de Fedorov o poliedro de Kelvin |
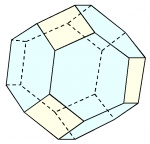 |
24 | 90° - 120° - 120° | 36 | √10a ≅ 3,2a | 14 | 6 cuadrados 8 exágonos |
Oh | [7] |
| Rombicuboctaedro o rombicuboctaedro menor |
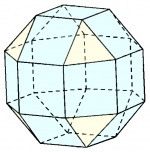 |
24 | 60° - 90° -90° - 90° | 48 | 26 | 8 triángulos 18 cuadrados |
Oh | [8] | |
| Nombre | Imagen | Vértices | Ángulos en vértices |
Aristas | D[9] | Caras | Tipos de caras |
Grupo puntual |
Fuentes |
| Cubo romo o cuboctaedro romo (2 enantiomorfos) |
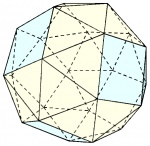 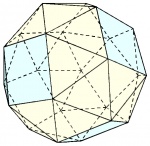 |
24 | 60° - 60° - 60° - 60° - 90° | 60 |  |
38 | 6 cuadrados 32 triángulos |
O | [10] |
| Icosidodecaedro o triakontágono |
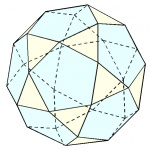 |
30 | 60° - 108° - 60° - 108° | 60 | 32 | 12 pentágonos 20 triángulos |
Ih | [11] | |
| Cuboctaedro truncado o rombicuboctaedro mayor |
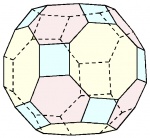 |
48 | 90° - 120° - 135° o 90° - 135° - 120° |
72 | 26 | 6 octógonos 8 exágonos 12 cuadrados |
Oh | [12] | |
| Dodecaedro truncado | 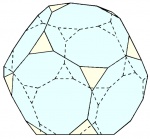 |
60 | 60° - 144° - 144° | 90 | 32 | 12 decágonos 20 triángulos |
Ih | [13] | |
| Nombre | Imagen | Vértices | Ángulos en vértices |
Aristas | D[14] | Caras | Tipos de caras |
Grupo puntual |
Fuentes |
| Icosaedro truncado | 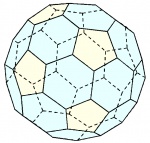 |
60 | 108° - 120° - 120° | 90 | |
32 | 20 exágonos 12 pentágonos |
Ih | [15] |
| Rombicosidodecaedro o rombicosidodecaedro menor |
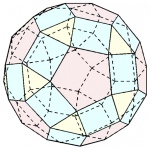 |
60 | 60° - 90° - 108° - 90° | 120 | 62 | 12 pentágonos 30 cuadrados 20 triángulos |
Ih | [[16]] | |
| Dodecaedro romo o icosidodecaedro romo (2 enantiomorfos) |
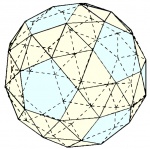 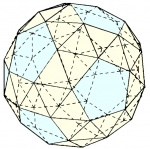 |
60 | 60° - 60° - 60° - 60° - 108° | 150 | ≅ 4,3a | 92 | 12 pentágonos 80 triángulos |
I | [17] |
| Icosidodecaedro truncado o rombicosidodecaedro mayor |
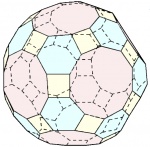 |
120 | 90° - 120° - 144° o 90° - 144° - 120° |
180 | 62 | 12 decágonos 20 exágonos 30 cuadrados |
Ih | [18] | |
| Nombre | Imagen | Vértices | Ángulos en vértices |
Aristas | D[19] | Caras | Tipos de caras |
Grupo puntual |
Fuentes |
Algunas aplicaciones prácticas
- Cubo romo: cúpula bizantina sobre pechinas (en rigor, la superficie se obtiene de la intersección de la esfera que inscribe al cubo romo con el cubo del cual éste se obtiene por truncamiento).
- Icosaedro truncado: cúpulas geodésicas; pelotas de fútbol.
- Octaedro truncado: único poliedro semirregular capaz de llenar por repetición un volumen sin dejar intersticios.
- Rombicuboctaedro: forma antigua de faroles que llegó a ser usado en algunos de los primeros automóviles.
- Rombicosidodecaedro: cúpulas geodésicas; estructura de los fullerenos.
Fuentes
- Archimedean solid en WolframMathworld.
- Ghyka, Matila; Estética de las proporciones en la naturaleza y en las artes; Editorial Poseidón; ciudad de Buenos Aires; 1953; Ghyka EPNA; pp. 87‑95. Discute interesantes usos artísticos pero la terminología no siempre es matemáticamente correcta.
- Archimedean solid en Wikipedia en inglés.
- Uzquiano, Gabriel; ¿Qué es un poliedro?; revista Investigación y Ciencia; septiembre 2011; pp. 91‑93.
Véase también
