Cómo armar poliedros

Figura 1. Pantalla de lámpara con estructura de
rombicuboctaedro hecha con esquineros.

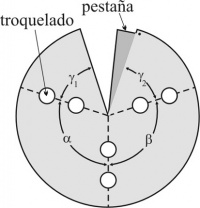
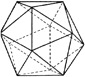
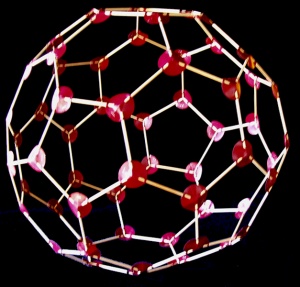
Se explica aquí cómo armar poliedros con varillas y esquineros, técnica que tiene al menos 2 funciones importantes. La primera es facilitar la asimilación del importante concepto abstracto de estructura mediante su realización concreta en el caso geométrico de los poliedros, donde los elementos son las aristas (varillas) y las relaciones son los ángulos entre aristas (determinados por los ojales de los esquineros que las sujetan) y las distancias entre vértices (dados por la longitud de las varillas). La segunda aplicación es permitir al docente disponer de conjuntos de cuerpos fácilmente transportables sin el riesgo de rotura de los hechos de otros modos. Se explican aquí todos los pasos a seguir para la construcción de cualquier poliedro —regular o no, convexo o no— y se dan sugerencias sobre materiales que pueden usarse en la tarea, incluyendo algunos reciclados. Se dan los esquineros que permiten la construcción de los 5 sólidos platónicos (tetraedro, cubo, octaedro, icosaedro y dodecaedro) y de algunos de los bellos poliedros arquimedeanos, como el ilustrado en la Figura 1. En estas categorías de poliedros, para los cuales los esquineros son todos similares y las varillas tienen todas la misma longitud, se obtiene al mismo tiempo una prueba constructiva de que están unívocamente determinados por los ángulos poliedros y la longitud de arista, conceptos geométricos de valor práctico.

Materiales, útiles, técnicas e información requeridas

• Materiales
  • esquineros: envases TetraPak® reciclados o tapas de fotocopias anilladas en desuso o cartulina semigruesa plastificada.
  • aristas: varillas para brochettes de buena calidad o varillas de madera torneada.
  • adhesivo en barra
  • 1 hoja de papel de lija Nº 120.
• Útiles
  • calibre;
  • tijera;
  • trincheta;
  • sacabocados del diámetro (holgado) de las varillas a usar;
  • abrochadora chica.
• Información
  • propiedades geométricas del poliedros a armar: Nº de vértices y aristas, ángulos poliedros en cada vértice;
  • patrones de los esquineros requeridos.
• Técnicas
  • corte con trincheta;
  • troquelado con sacabocados;
  • abrochado con abrochadora;
  • medición de diámetros de varillas con calibre;
  • medición de ángulos con transportador (para hacer los patrones de esquineros no dados aquí).

Método y recomendaciones de construcción

El método de construcción es la unión de varillas de madera (las aristas del poliedro) con esquineros que las sujetan para formar el ángulo poliedro correcto en cada vértice. Para las varillas conviene usar palitos de brochette, que tienen usualmente unos 4 mm de diámetro y 24 cm de longitud y son de bajo costo y gran dureza, aunque a veces se rajan. Las de baja calidad no son recomendables porque suelen ser torcidas, de superficie rugosa y de diámetros no uniformes. Si las usa, tenga cuidado de seleccionar sólo las bien rectas y del mismo diámetro, ya que el mismo es crítico para el buen funcionamiento de los esquineros. Pueden usarse varillas de madera torneada, usualmente disponibles en comercios de productos de madera, que no tienen estos problemas pero son mucho más caras y usualmente menos resistentes.

Las varillas deben recortarse de una longitud a apropiada al tamaño final del cuerpo que se quiere construir. Para los sólidos regulares y semirregulares este largo puede obtenerse a partir del valor del diámetro de la esfera D que los circunscribe, valor dado en la Tabla 1 y la del artículo poliedros arquimedeanos. Por ejemplo, si se quiere construir la estructura de una pelota clásica de fútbol (icosaedro truncado) de un tamaño comparable a la verdadera (unos 22 cm) el valor es D=5a. Esto da para a un valor de unos 4,8 cm. La de la Figura 5 se construyó con varillas de 12 cm, resultando un diámetro final de 57,5 cm.

Los esquineros delimitan los ángulos poliedros en cada vértice, por lo que deben ser capaces de conservar bien su forma (tener suficiente rigidez), así como sostener con firmeza y sin desgarrarse las varillas que atraviesan sus ojales. El material más barato que cumple estas condiciones es el laminado usado en los envases TetraPak®. Es más resistente y de mejor presentación el material con que se hacen las tapas de documentos fotocopiados y anillados. Las tapas de cuaderno, otro material reciclable, suelen ser demasiado gruesas, poco flexibles y fácilmente desgarrables, aunque ésto no es regla general.

En los poliedros convexos regulares y arquimedeanos (ver Tabla 1) las aristas determinan ángulos poliedros por confluencia de por lo menos 3 y no más de 5 caras en cada vértice. La razón de esta limitación es que en estos poliedros el menor ángulo interno de una cara es 60° (triángulo equilátero), el número mínimo de caras en un vértice es 3 (de lo contrario se delimita un plano, no un volumen) y pueden haber a lo sumo 5 triángulos equiláteros concurrentes en el mismo vértice para que el ángulo poliedro no sea plano (la suma de los ángulos internos de las caras en el vértice común debe ser menor de 360°).

Figura 2. Patrón genérico de esquinero para un triedro.

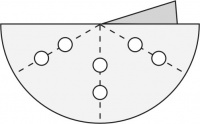
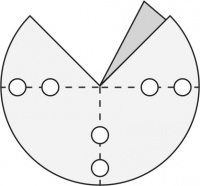
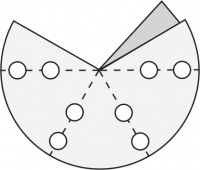
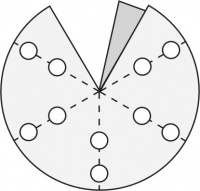
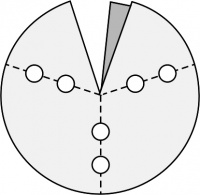
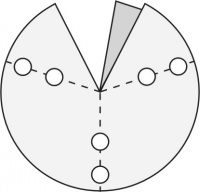
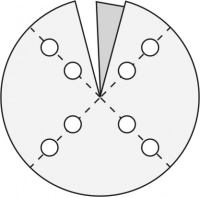
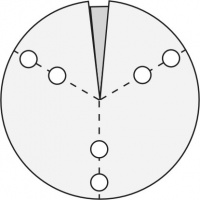
En cada vértice los ángulos entre aristas son los ángulos internos de las caras que concurren allí. El patrón general de un esquinero con tres aristas (triedro) es el de la Figura 2, fácilmente extensible a los de 4 y 5 aristas. La zona más oscura es la pestaña que permite fijar el borde opuesto por superposición y abrochado; es decir, debe quedar exactamente cubierta por el borde opuesto de la abertura. Los cortes deben efectuarse por las líneas continuas: con tijera por los bordes externos y con sacabocados para los ojales (los círculos blancos) por donde pasan las varillas. Se facilita el abrochado de la pestaña si se dobla levemente la esquina contigua a la pestaña señalada con un punto en la Figura 2. Éste sirve de tope al borde que se superpone cuando se lo abrocha para que tape exactamente la pestaña. Si el material ha sido bien elegido y el abrochado es bien hecho, no es necesario reforzar esta unión. Cuando sea indispensable hacerlo, use cemento de contacto o cola vinílica; la resina epoxi o el cianoacrilato no tienen buena adhesión en los materiales propuestos.

Los dobleces, marcados con líneas de trazos, corresponden a la posición de las varillas. Los ángulos alfa (α), beta (β) y gama (γ) de la Figura 2, donde

γ = γ₁ + γ₂,

son los ángulos internos de los 3 polígonos que tienen por vértice común el centro del esquinero (3, 4 o 5 en el caso general). Lo más efectivo y simple es elegir

γ₁ = γ₂= γ/2.

Ésto no siempre es posible, como en la estructura de la Figura 4, caso en que debe usarse esta libertad de elección. En base a consideraciones similares es fácil diseñar un esquinero para cualquier vértice, trátese o no de un poliedro convexo o regular, teniendo en cuenta que deben haber tantos dobleces y pares de ojales como aristas convergen en el vértice. Si la cara es un polígono regular de n lados, sus ángulos internos son todos iguales y valen α = (n – 2)·180°/n. Por ejemplo, el esquinero correspondiente a un cubo (las caras son cuadrados con n=4) tiene los siguientes ángulos:

α = β = γ = 90°, γ₁ = γ₂ = 45°

y hay tantos dobleces como aristas, 3. Aunque los ejemplos dados más adelante corresponden a poliedros regulares o arquimedeanos, con las modificaciones que correspondan el método permite construir esquineros para cualquier poliedro. La diferencia principal del caso general con los poliedros regulares y semirregulares es que en los últimos los esquineros son todos similares, mientras que en los primeros hay que hacer uno diferente para cada vértice. En la sección Esquineros selectos se dan los patrones correspondientes a todos los sólidos platónicos y algunos de los poliedros arquimedeanos.

Como guía para todos los cortes y dobleces se usan fotocopias del patrón pegadas con unos pocos toques de adhesivo sólido (no use otro, pues se busca poca adherencia) sobre la cara del material que no será visible cuando el poliedro esté terminado. Para obtener con eficiencia todos los necesarios, haga fotocopias con tantos ejemplares del patrón como esquineros se quieren cortar, cantidad igual al número de vértices del poliedro. En la siguiente sección se da una técnica para lograr ésto eficientemente.

Figura 3. Varilla insertada en esquinero.

Los ojales circulares, por donde se pasarán las varillas del modo ilustrado en la Figura 3, deben troquelarse con un sacabocados de diámetro levemente superior al de las varillas. Pruebe con un esquinero armado, si cuesta mucho introducir la varilla, aumente el diámetro de los agujeros a la medida siguiente, verificando que no se suelte. La razón principal por la que el material del esquinero no debe ser demasiado grueso es facilitar la formación en su interior de la presilla que sujeta a la varilla. Esto se ilustra en dicha figura, donde la fotografía de la izquierda muestra la parte interior del esquinero (cara cóncava) y la derecha la exterior (cara convexa). De este modo las varillas concurren en el vértice por la parte interior del esquinero. La mayor deformación se localiza en los ojales, donde el riesgo de rotura es máximo. Para evitar esta rotura es que los ojales se hacen circulares en vez de cuadrados, caso en que los desgarramientos de sus esquinas serían frecuentes.

Una vez finalizados los cortes, debe eliminarse completamente de los esquineros el papel con los patrones, humedeciéndolo si es necesario. Los ojales deben conformarse previamente al armado final, usando una varilla. Para terminar prolijamente esta tarea conviene "planchar" la zona contigua a los ojales con algún objeto suave, como el cuerpo/tapa de un bolígrafo o marcador, de modo de eliminar las inevitables arrugas del material. Se fijan entonces los esquineros con la abrochadora, cuidando de tapar exactamente la pestaña, que debe quedar del lado interior (cóncavo) del esquinero.

Una vez armados todos los esquineros (el orden es aquí indiferente y esta etapa podría ser anterior o hecha en paralelo, simultáneamente) hay que cortar, con trincheta, todas las varillas de la misma longitud y redondear sus extremos para facilitar la introducción. Conviene hacer ésto con ayuda de un sacapuntas (no hay que afilarlos, sólo redondear levemente los extremos) y retocar con un poco de papel de lija mediano, Nº 120 o similar. Se introducen luego ordenadamente las varillas en los esquineros, verificando con la imagen del poliedro la correcta formación de las caras. Los dos errores más comunes de esta etapa de armado final son de orientación del esquinero. Estos errores pueden suceder de 2 modos diferentes: cuando se orienta un esquinero hacia afuera de lo que será la estructura final, violando la condición de poliedro convexo; cuando, por ejemplo, en un icosaedro truncado se delimita una cara pentagonal con un ángulo interno que corresponde a una exagonal.

Las estructuras construidas por este método, aunque sólo soportan su propio peso, brindan formas muy variadas con mínimo gasto en materiales. Se requieren, eso sí, paciencia y prolijidad para fabricar bien los esquineros apropiados para cada vértice y conformar bien las varillas. Cuando no se las usa, estas estructuras pueden desarmarse y guardarse ocupando un volumen muy reducido, lo que es muy práctico. Sólo deben pegarse las varillas a los esquineros cuando se quiere una estructura permanente que no se deforme, lo que puede suceder cuando se las manipula con frecuencia.

Impresión de patrones

Es fácil recortar los esquineros cuando se usa un patron de guía para cada uno. Para eso se necesitan tantos patrones como esquineros hay, es decir, como vértices tiene la estructura (véase la Tabla 1 para los poliedros regulares y algunos semirregulares). El número de fotocopias a hacer se disminuye drásticamente si se usa la siguiente técnica:

• Se hace primero el patrón y luego se lo fotocopia (1 fotocopia hecha; 2 patrones).
• Recortando el patrón copiado se lo pega sobre una hoja junto al original y separado de él unos 2 mm y se los fotocopia (2 fotocopias hechas; 4 patrones).
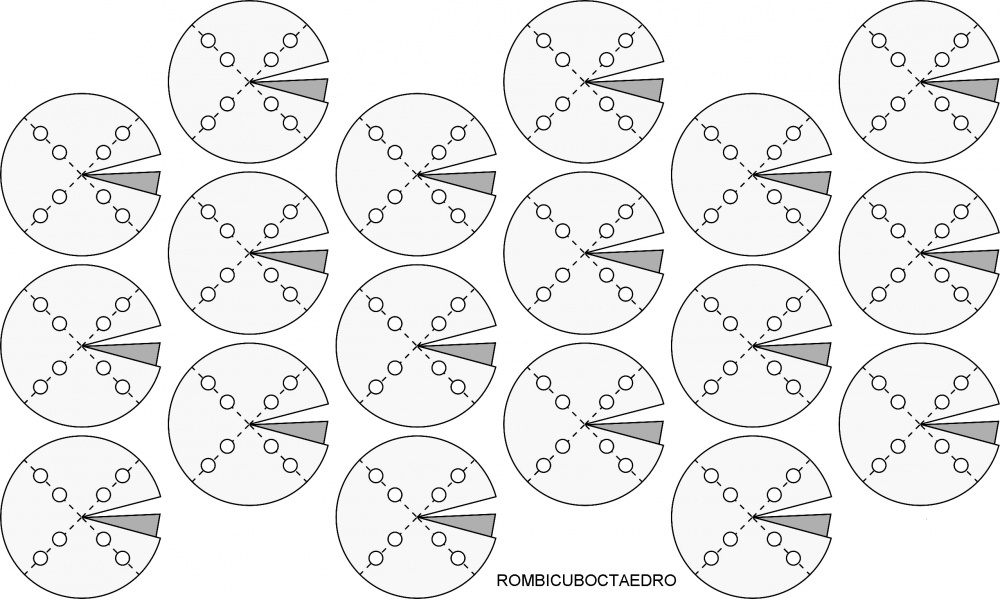
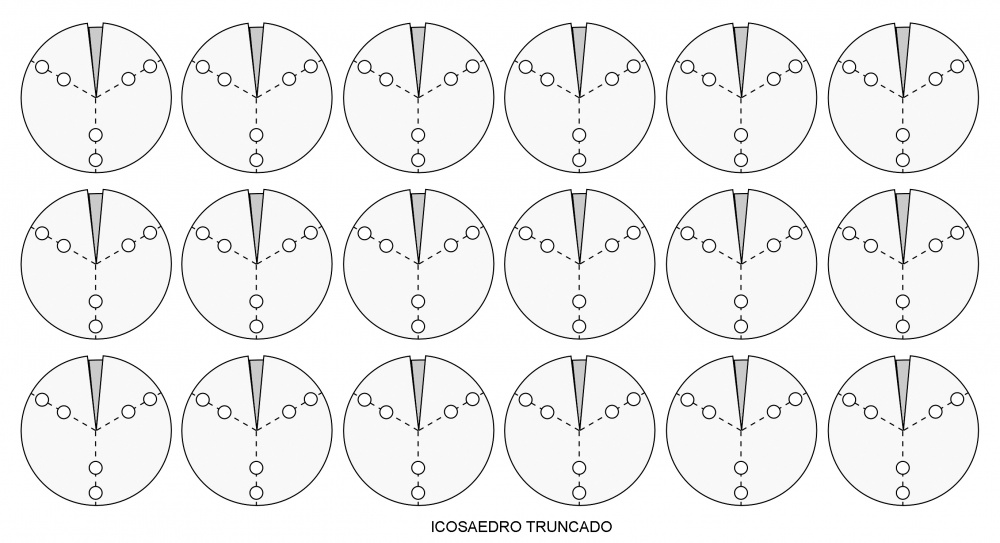
• Se fotocopian luego 3 de los 4 patrones que ya se tienen, formando una línea, como en las 2 hojas al final del artículo (3 fotocopias; 7 ejemplares).
• En la siguiente etapa se pueden fotocopiar 2 líneas completas y en la subsiguiente, 4, con lo que en la fotocopia subsiguiente se llega al límite del tamaño de la hoja (6 fotocopias; 25 patrones), ya que una hoja de formato legal (21,5 cm·35,6 cm), la mayor de las fáciles de conseguir, puede contener 18 patrones.
• De allí en más se fotocopian hojas completas, tantas como sean necesarias y algunas más para reemplazo en caso de error.

La técnica es muy eficiente en disminuir el número de fotocopias. Para hacer los patrones de los 90 esquineros necesarios para la estructura de la pelota de fútbol, se requieren sólo 10 fotocopias sucesivas y sobran 7 patrones de reemplazo. Si se tiene una PC, un digitalizador y un programa de procesamiento de gráficos, se puede armar la hoja completa de patrones de una sola vez, lo cual reduce el número de fotocopias a hacer a sólo 6. Si, en cambio, se fotocopiaran sólo patrones individuales, habría que hacer 96 fotocopias para obtener la misma cantidad final.

Poliedros regulares y semirregulares

Figura 4. Rueda gigante hecha con esquineros de TetraPak® con estructura de prisma recto octogonal.

Los cuerpos más fáciles de armar con esta técnica son aquellos cuyos angulos poliedros (los que forman las caras en cada vértice) son congruentes (superponibles por traslaciones, rotaciones y, eventualmente, reflexiones). Esto equivale a decir que los esquineros son todos idénticos, ya que pueden armarse con cualquiera de sus 2 superficies hacia el interior, lo que equivale a una reflexión. La condición de congruencia parece forzada, pero esto proviene de una pobre comprensión de lo que es un sólido regular o semirregular. Los sólidos platónicos son frecuentemente considerados como los únicos cuyas caras son polígonos regulares idénticos, lo que es falso, ya que a esa condición hay la de congruencia. Por ejemplo, hay 8 poliedros diferentes cuyas caras son todas triángulos equiláteros, denominados deltaedros. De ellos sólo 2 tienen todos sus ángulos poliedros congruentes: el tetraedro regular, el octaedro regular y el icosaedro regular, los 3 sólidos platónicos cuyas caras son triángulos equiláteros.

De especial interés en la construcción de modelos a escala son los prismas rectos cuyas caras pueden o no ser polígonos regulares. Muchos de estos poliedros también tienen la propiedad de tener esquineros idénticos, como se ilustra con el caso de la rueda gigante de la Figura 4. Los esquineros del cubo (véase a pie de página) permiten construir cubículos muy variados cuyas caras son rectángulos que pueden tener cualquier proporción deseada.

En la tabla inferior se dan los datos necesarios para construir los esquineros de todos los sólidos platónicos y algunos de los arquimedeanos. Algunos de sus patrones se dan al pie de página, quedando los restantes como ejercicio para el lector.

Poliedro	Imagen	Vértices	Aristas	Angulos poliedros
tetraedro		4	6	60°; 60°; 60°
cubo		8	12	90°; 90°; 90°
octaedro		6	12	60°; 60°; 60°; 60°
icosaedro		12	30	60°; 60°; 60°; 60°; 60°
dodecaedro		20	30	108°; 108°; 108°
cuboctaedro		12	24	60°; 90°; 60°; 90°
rombicuboctaedro		24	48	60°; 90°; 90°; 90°
octaedro truncado		24	36	90°; 120°; 120°
icosidodecaedro		30	60	60°; 108°; 60°; 108°
icosaedro truncado		60	90	108°; 120°; 120°
Tabla 1. Datos de los sólidos platónicos y algunos arquimedeanos.

Etapas del armado de una estructura

Figura 5. Icosaedro truncado
hecho con el método aquí descripto.

Como cualquier técnica, se requiere algo de práctica para llevarla a cabo bien. Se recomienda por eso comenzar armando una estructura con algunos de los patrones aquí dados, antes de intentar diseñar patrones nuevos. En el caso general, las etapas principales del armado de un poliedro son las siguientes:

• Determine los ángulos internos de las caras que tienen un vértice en común.
• Cuente la cantidad de vértices de cada tipo diferente y use o diseñe el patrón correspondiente a cada uno.
• Haga la cantidad necesaria de patrones de cada tipo y algunos más.
• Seleccione la cantidad necesaria de varillas (Nº de aristas) usando el calibre para verificar que todas tienen el mismo diámetro.
• Determine la longitud de varilla apropiada para la estructura.
• Corte todas las varillas de la misma longitud, redondeando sus extremos.
• Recorte los patrones unos milímetros por fuera de su borde.
• Pegue los patrones con unos pocos toques de adhesivo sólido sobre el lado del esquinero que quedará en el interior.
• Recorte luego cuidadosamente con tijera por las líneas continuas exteriores. Respete el receso de la pestaña.
• Corte los ojales con un sacabocados de diámetro levemente superior al de las varillas.
• Despegue los patrones.
• Abroche los esquineros.
• Forme las presillas de los esquineros, eliminando las arrugas.
• Arme el cuerpo completando un ángulo poliedro por vez.

Esquineros selectos

• 

  Tetraedro.

• 

  Cubo.

• 

  Octaedro.

• 

  Icosaedro.

• 

  Dodecaedro.

• 

  Octaedro truncado.

• 

  Rombicuboctaedro.

• 

  Icosaedro truncado.

Hoja tamaño oficio de esquineros del rombicuboctaedro.

Hoja tamaño legal de esquineros del icosaedro truncado.

Fuentes

La técnica aquí descripta fue desarrollada por Carlos E. Solivérez para los cursos de Tecnología del Instituto de Formación Docente de San Carlos de Bariloche, entre los años 2000 y 2004.

Véase también

• Poliedros arquimedeanos.

---